Interpolator Overload Distortion

Most digital playback devices include digital interpolators. These interpolators increase the sample rate of the incoming audio to improve the performance of the playback system. Interpolators are essential in oversampled sigma-delta D/A converters, and in sample rate converters. In general, interpolators have vastly improved the performance of audio D/A converters by eliminating the need for analog brick wall filters. Nevertheless, digital interpolators have brick wall digital filters that can produce unique distortion signatures when they are overloaded.

10% Distortion

An interpolator that performs wonderfully when tested with standard test tones, may overload severely when playing the inter-sample musical peaks that are captured on a typical CD. In our tests, we observed THD+N levels exceeding 10% while interpolator overloads were occurring. The highest levels were produced by devices that included ASRC sample rate converters.

Most CDs Have Peaks that Exceed 0 dBFS

In prior papers, I have shown that many CDs have inter-sample peaks that exceed 0 dBFS. This can occur even when none of the actual samples reach the maximum positive and/or negative digital codes. We can scan a track and reconstruct the recorded waveform to determine the "true peak" level of the original waveform.

Inter-sample peaks exceeding 0 dBFS often occur thousands of times per track (as shown in Figure 1). This characteristic is common in many genres of music, and it is not necessarily caused by excessively loud recordings.

Figure 1 - CD Track - Peaks Exceeding 0 dBFS are Highlighted in Red

Several individuals have scanned their music servers to measure the true-peak levels of each stored track. This initial data set shows that most CD tracks have true-peak levels of about +1 dBFS. This is 1 dB (about 1.2:1) above the values associated with the maximum and minimum digital codes. Some CD tracks measure +2 dBFS (1.26:1) and a small minority measure close to +3 dBFS (1.4:1). In a few very rare cases, tracks have isolated transients that exceed +3 dBFS.

The server scans also show that MP3 compressed tracks have higher true-peak amplitudes than the original tracks.

It would be great if we had a comprehensive database of true-peak measurements for a larger library of CD tracks, but this does not yet exist. Nevertheless, we have enough evidence to show that we need about 3 dB of headroom above 0 dBFS. This would allow us to play the vast majority of CD tracks without adding distortion. This headroom is especially important when playing MP3 tracks or streamed MP3s.

Unique IMD Signature Produced by Interpolator Overloads

When a fixed-point interpolation filter overloads it doesn't just clip the peaks of the waveform. Instead, the overload causes a partial or complete failure of the interpolator's low-pass function. The interpolator's brick wall low-pass filter essentially disappears, and the stopband attenuation approaches 0 dB. IMD sum and difference products are created by the interactions between the input sample rate, the output sample rate, and the audio content.

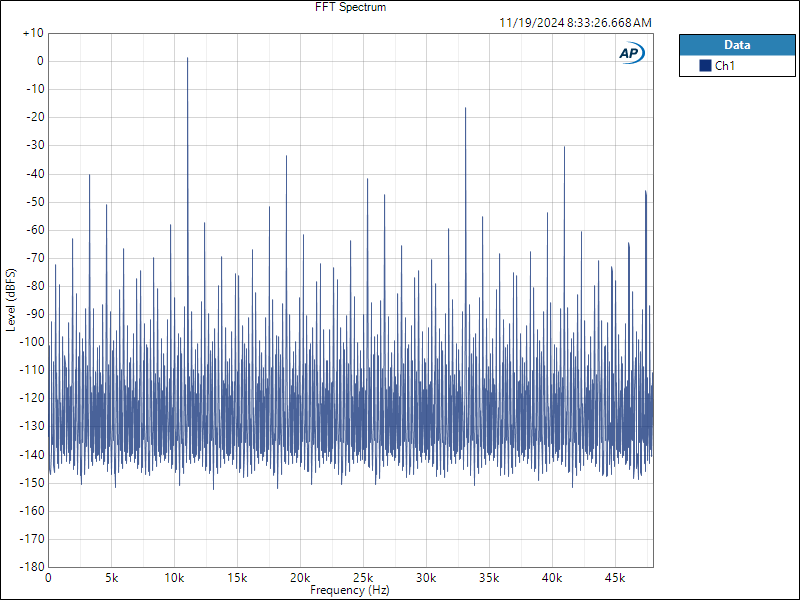
We ran a +3.01 dBFS test tone through a digital-to-digital DSP device (miniDSP SHD Studio) and examined the output spectrum. This device includes a fixed-point ASRC. The output spectrum showed high-level distortion products splattered across the entire audio band. These high-amplitude distortion products extended into the ultrasonic region between 20 kHz and 48 kHz (see figure 2). Figure 3 shows the same device when the test signal was reduced just enough to eliminate the overloads (0 dBFS). In both cases, the test tone was an 11.025 kHz sinewave. The ASRC delivers a THD+N of better than -130 dB when operating normally (figure 3), but this jumps to -17.5 dB when overloaded (figure 2).

Figure 2 - ASRC Interpolator Overload Distortion Spectrum at +3.01 dBFS

Figure 3 - ASRC Output Spectrum at 0 dBFS (No Overloads)

If interpolator overloads were simply clipping the waveform, we would expect to see a series of harmonics above the frequency of test tone (see figure 4). Instead, we see IMD products scattered over the entire spectrum starting in the low bass and ending in ultrasonic frequencies at up to 1/2 of the interpolator's output sample rate (see figure 2). These high-amplitude IMD products may not be fully masked by music.

Audibility Tests

To gain some understanding of the audibility we conducted listening tests using sinusoidal test tones. In our listening tests we stimulated interpolator overloads using a continuous high-amplitude 11.025 kHz sinewave. The resulting interpolator overloads produced IMD distortion across the entire audio band (see figure 2). The distortion included high-amplitude bass and midrange tones that were easy to hear. In our listening tests, it was very easy to hear the difference between the output spectrum shown in figures 2 and 3. This listening test proves that interpolator overload distortion can be heard under the right conditions.

Figure 4 - Analog Clipping at a 3dB Overload

If simple clipping had occurred, we would have produced odd and even harmonics of the 11.026 kHz sinewave (see figure 4). Notice that the harmonics are all above the 20 kHz range of normal hearing. For this reason, it would be nearly impossible to hear the difference between a clean 11.025 kHz sinewave and a clipped 11.025 kHz sinewave. In contrast, it is easy to hear the difference between the spectrum of figure 2 (interpolator overload distortion) and figure 4 (analog clipping). Figure 4 sounds clean, figure 2 sounds nasty. No golden ears required!

The important takeaway is that ASRC interpolator overloads do not create harmonic distortion (figure 4). Instead, they splatter non-harmonic distortion products across the entire output spectrum (figure 2).

Audibility in Music

If we can hear the audible distortion effects produced by a continuous tone (figure 2), this suggests that audible distortion effects could be produced when playing music. How audible? Nobody knows. The overloads are usually transient events, and the music should mask some of the distortion some of the time. Nevertheless, there are many variables and millions of music tracks that we could analyze.

Music can cause overloads even if it has no content at the worst case 11.025 kHz frequency. For example, multi-sample sustained overloads can be caused by square waves of any frequency. Tones at 1/8 and 1/16 of the sample rate are also problematic. Recordings that used hard analog limiting could stimulate interpolator distortion due to the clipped high amplitude waveforms in the recording. In other words, the interpolator overloads could make clipped music sound worse than it should. It is even possible that it could also expose clipping that would otherwise be inaudible.

The audibility of these effects has not been proven or disproven in the context of recorded music. At the present time, there is no agreement on the audibility of interpolator overload distortion when playing music.

Given the lack of any known audibility thresholds, it may be wise to take a conservative approach:

At Benchmark, we always attempt to keep electronically produced distortion artifacts below the threshold of hearing. We believe that we should not use music to mask defects in our electronics. Instead, we design our electronics so that they do not produce errors exceeding the 0 dBSPL threshold of hearing at the output of our speakers. If our electronics are properly designed, we should only hear the distortion produced by the speakers and the distortion captured in the recording. The goal is to keep the distortion residual produced by the playback electronics below 0 dBSPL at the listening position. Benchmark products, and many other state-of-the-art audio products, meet or exceed this ambitious goal.

If we can eliminate a problem, we don't need to worry about determining audibility thresholds.

Some Playback Devices do not Overload

In our tests some playback devices rendered every musical peak without adding distortion. These devices had high-headroom interpolators which provided at least 3.01 dB of headroom above 0 dBFS. This is exactly enough headroom to handle the worst case (+3.01 dBFS) continuous sinusoidal tone. In figure 5, the red curve shows a clean output spectrum from a Benchmark DAC3 which has a high-headroom asynchronous interpolator. The blue curve shows the asynchronous interpolator overload distortion from the much older Benchmark DAC1. The digital headroom in the DAC3 is 3.01 dB but the first-generation DAC1 had no digital headroom.

Figure 5 - +3.01 dBFS Test - DAC3 - Red, DAC1 - Blue

The headroom in the DAC1 cannot be fixed with a hardware or software update, but there are some workarounds that will eliminate the digital overload distortion. The distortion can be eliminated if the digital audio is turned down by at least 3 dB before it is fed to the DAC1. In many cases, this can be done using the digital volume control in an audiophile-grade music player. When this 3 dB volume reduction is applied, the DAC1 plays cleanly (see figure 6). If you have a DAC1 and you play music from a fixed-gain disk player, you should consider replacing the DAC1 with a DAC3.

Figure 6 - Input Level Reduced by 3 dB - DAC3 - Red, DAC1 - Blue

Figure 6 shows the 11.025 kHz test tone being played at 0 dBFS instead of +3.01 dBFS. When this signal is reduced to 0 dBFS, the DAC1 delivers a clean output spectrum (blue curve). The difference between noise shown in the red and blue traces demonstrates the technological improvements made over a 10-year time span. But notice that the improvements in the noise floor are much less significant than the elimination of the interpolator overload problem. This suggests that the most audible difference between the DAC1 and the DAC3 could be the elimination of the interpolator overload distortion. Curiously, very few manufacturers and very few independent labs publish tests for interpolator overload distortion, and many DACs still have this problem! Without test reports, it is hard to know what you are really buying.

Testing for Interpolator Headroom

Interpolator headroom cannot be measured with traditional audio tests. A playback system may look nearly perfect when conducting a full suite of traditional tests but fail miserably when using special peak overload test tones.

Figure 7 - +3.01 dBFS Waveform with Peaks Between Samples

It is possible to create a +3.01 dBFS sinusoidal tone at exactly 1/4 of the sample rate (see figure 7). This higher-than-normal amplitude can only be achieved when the waveform peaks fall exactly halfway between successive samples. If these samples reach the maximum digital code, the inter-sample peaks will reach a level that is 1.414 times as high, or 3.01 dB higher than the samples. This +3.01 dBFS test tone is the highest amplitude continuous sinusoidal tone that can be transmitted over a PCM digital system. There are other continuous signals, such as wideband square waves, that can generate peaks exceeding +2 dBFS but these are not as useful for making quantitative measurements. Nevertheless, wideband square waves can be used to run quick checks for overloads.

At a 44.1 kHz CD sample rate, the required sinusoidal frequency is 11.025 kHz. Some systems will pass this+3.01 dBFS tone without distorting. "Defective" systems may produce more than 10% IMD while playing this tone.

Headroom Measurements

The amplitude of the +3.01 dBFS test tone can be reduced with a digital volume control to determine exactly how much headroom a system has. The digital headroom in some systems may exceed 0 dB but fall short of 3.01 dB. Digital headroom should be a standard specification on a digital device.

Volume Control Measurements

If a playback device has a digital volume control, test the device with a +3.01 dBFS tone. If the device has an interpolator overload problem, this may go away when the digital volume control is turned down. However, in many cases, you will discover that the volume control is located after the interpolator. If this is the case, you will find that the overload distortion is present at all volume settings!

Never assume that a built-in digital volume control will fix an interpolator overload problem. Many DSP devices have a fixed-point ASRC device on every digital input to the DSP. The digital volume is implemented inside the DSP, after the signal has already passed through the fixed-point ASRC. The damage done by the interpolator in the ASRC cannot be undone by downstream volume controls.

The DAC1 had an analog volume control after the output of the sigma-delta D/A converter. The ASRC interpolator and the D/A interpolator are both located ahead of the volume control. Because of this topology, the interpolator overload distortion is present at all volume settings.

The DAC3 has a digital volume control that includes a maximum gain boost of +3 dB. At the calibrated 0 dB bypass setting, the DAC3 will not overload. But it can be overloaded if the volume is set between +0.5 dB and +3.0 dB.

Spectral Analysis

The overload spectrum shown in figure 2 (D-to-D ASRC) is different than the overload spectrum shown in figure 5 (DAC1). Each DAC or DSP that has an overload problem will produce a spectrum that may help reveal any intermediate or final oversampling rates. If the output spectrum looks like figure 4, the device may just have an analog clipping problem, and this is probably less serious than an overloaded interpolator.

Stepped Level THD+N Sweeps

When writing this paper, I wanted to include a stepped THD+N vs. level sweep using the +3.01 dBFS sinewave. Such a sweep would show the onset of interpolator overloads in an easy-to-read graph.

At the current time, the Audio Precision APx555b test set cannot run stepped level sweeps when using the custom waveform playback function. I will be discussing this with AP. I would like to see them add an Fs/4 +3.01 dBFS test tone and I would like to see them add the ability to run stepped sweeps using custom waveforms.

Summary

The interpolators in oversampled D/A converters and sample rate converters can overload when driven with high inter-sample peaks. True-peak levels above 0 dBFS often occur in recorded music. Low sample rate recordings have the highest incidence of true-peak levels exceeding 0 dBFS. CD recordings often have thousands of these peaks on each track.

When interpolators overload, the brick-wall low-pass filters cease operating as filters. When this happens, high-amplitude IMD products are often splattered across the entire output spectrum. This distortion does not resemble the distortion produced by analog clipping. Instead, the distortion is non-harmonic and non-musical. The worst offenders seem to be devices that include fixed-point ASRC devices. Nevertheless, these ASRC devices can be transparent if the audio is attenuated before passing through the ASRC. The DAC3 is an example of a high-headroom design that includes an ASRC. An ASRC can provide many performance enhancements, but it must be engineered with adequate headroom.

Interpolator overloads can occur in many digital processing devices. When overloads occur in a digital processor, the distortion is baked into the output signal. This distortion cannot be removed once it is added to the music.

DSP devices, sample rate converters, and D/A converters should be tested with a +3.01 dBFS test tone. This tone should be added to audio test stations so that we can easily test and publish a standard set of digital headroom measurements.

Devices that overload should be avoided when possible. When this is not practical, the digital signal should be attenuated by 3 dB before it enters an offending device. If these steps cannot be taken, bursts of IMD will be produced whenever peaks exceed 0 dBFS. The audibility of these high-amplitude IMD bursts is unknown, but we can easily measure them. We have proven that we can easily hear this distortion when using +3.01 dBFS test tones. This suggests that the distortion should be audible with some music.

Benchmark takes a conservative approach to audibility. Our goal is to keep electronically generated noise and distortion below 0 dBSPL at the listening position. In other words, if it was possible to just play the distortion, it would not be loud enough to hear. This eliminates the need to mask electronic defects with music.

Unlike some forms of distortion, interpolator overload distortion can be completely eliminated. The digital system just needs to be designed with adequate headroom.

PDF Version