Buy one component and save 10% on up to 2 cables. Buy 2 components and get 4 free cables. Free shipping on USA orders over $700.
Buy one component and save 10% on up to 2 cables. Buy 2 components and get 4 free cables. Free shipping on USA orders over $700.
The Unique Evils of Digital Audio and How to Defeat Them
by John Siau August 25, 2010
Introduction
We are all too familiar with the criticisms of digital audio. We have heard digital audio described as harsh, brittle, lifeless, tense, cold, and non‐musical. Perhaps each of us can add our own adjectives to this list. We are surrounded by poor‐quality digital systems. Our consumer‐grade CD players, DVD players, HDTV sets, and portable media players are usually equipped with the least expensive digital converters available. We all know that these devices are lacking the “perfect sound forever” that was attributed to the CD in 1982.
- Is digital audio fundamentally flawed?
- Have we followed the wrong path for the past 28 years?
- Should we go back to analog audio systems?
- Has anything improved in 28 years?
- How good can digital audio get?
To answer these questions, we will look at the root causes of distortion and noise in digital systems. We will examine how these differ from the distortion and noise in analog systems. Most importantly, we will look at the effectiveness of today’s solutions to these digital problems.
Harmonic Distortion is Dominant in Analog Systems
All musical instruments and human voices produce a rich spectrum of harmonics (also known as overtones). These harmonics give warmth and character to musical sources. The harmonics of a violin distinguish its sound from that of a trumpet. Analog systems always add some harmonic distortion (measured as THD) but this distortion produces harmonics that fall directly on top of the harmonics that naturally occur in musical sources.
Harmonic distortion can be hard to detect and may even add warmth to some musical sources. In some cases, harmonic distortion can reach relatively high levels before it begins to change the sound of an instrument. Even when audible, these subtle changes to the sound of an instrument can be difficult to recognize without substantial exposure to the live unamplified instrument.
Some Analog Systems Suffer from IMD – More Audible than THD
Analog systems often introduce small amounts of IMD (inter‐modulation distortion). For a given level, IMD is normally much more audible than THD. Harmonic distortion mimics the natural overtones of musical instruments while IMD produces distortion tones that have no harmonic relationship to the music. Analog systems with slew‐rate problems may suffer from excessive IMD. Circuits with RF (radio frequency) instability and susceptibility may also introduce IMD.
IMD can be reduced to insignificant levels with good circuit design techniques. Many early transistorized audio devices (produced in the ‘60s and ‘70s) suffered from high IMD due to the limitations of available components. Today we have a rich selection of high‐quality audio op‐amps and IMD problems are much less common. There are some modern op‐amps that have insufficient slew rates to support audio, but these usually only find their way into low‐cost products. Significant levels of IMD are inexcusable in modern high‐end analog equipment.
Digitally-Induced Distortion often Resembles IMD
In many ways, the distortion caused by digital systems is very similar to the IMD
produced by early transistorized audio devices and some of today’s low‐cost audio equipment. Like IMD, digitally‐induced distortion can occur anywhere in the audio band. Digital distortion artifacts often occur at tones that are absent from the live musical source. Digital distortion artifacts may occur above and below a note being played. These distortion artifacts are not masked by the natural harmonics of the instruments and therefore are much more noticeable and much more disturbing than harmonic distortion.
Unique Causes of Distortion in Digital Systems – The “Evils” of Digital
There are several mechanisms that produce distortion signatures that are unique to digital systems. These mechanisms include; jitter, quantization errors, and aliasing. We will look at each of these digital “evils” to determine our strategy. Can we attack these “evils” successfully, or should we retreat from the digital domain and return to the safety and comfort of our analog systems?
“Evil” #1 - Jitter
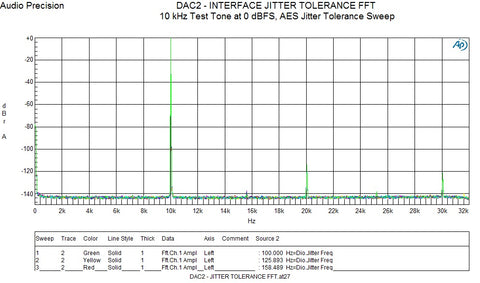
Jitter is a variation in the time interval between one sample and the next. To work properly, a digital system must have a known time‐interval between each successive sample. If this time‐interval varies in an A/D converter, the input signal is sampled at the wrong time and an amplitude error occurs. Timing‐errors in a D/A converter produce the correct amplitude at the wrong time. In both cases it can be shown that these errors “phase‐modulate” the audio.
Jitter Causes Phase Modulation
Vibrato is the musical term for phase modulation. It is a periodic variation in pitch. In concept, jitter produces effects similar to vibrato. Unfortunately there is usually nothing musically pleasing about the effects of jitter. We are all familiar with the low‐frequency phase‐modulation caused by wow and flutter. These were common with bad cassette tapes, cheap turntables, and old movie sound tracks. In many old movies it is possible to hear the pitch of the music flutter at the frame‐rate of the film. Jitter can cause a similar effect, but it may occur at many frequencies simultaneously. Jitter can cause a harsh, cluttered and unnatural sound long before it reaches obvious levels. SPDIF, AES, i2S, and other digital transmission formats tend to cause high‐frequency jitter at more than one frequency at a time. If this jitter is allowed to reach an A/D or D/A conversion circuit, phase‐modulation distortion will be produced.
Some Digital Systems have Audible Jitter‐Induced Distortion
Jitter is not a fundamental limitation of digital systems, it is simply a defect. The distortion caused by Jitter can be reduced to inaudible levels if the timing of A/D and D/A sampling is accurate enough. The timing accuracy required to guarantee inaudibility is rather surprising. Jitter must be reduced to about +/‐ 20 psec (+/‐ 20 trillionths of a second) to absolutely guarantee that it will never exceed the threshold of hearing at reasonably loud listening levels. Fortunately, a significant portion of the jitter-induced distortion is often masked by the music. Because of this masking, higher levels of jitter may be acceptable. There is still considerable debate about the thresholds for jitter audibility.
Some systems have enough jitter to easily reach audible levels. For example, many consumer devices have jitter that exceeds +/‐ 2 nsec (+/‐ 2 billionths of a second). Such a device will have jitter‐induced distortion that measures only 78 dB below peak audio levels. These consumer‐grade devices produce jitter induced artifacts that are well above the threshold of hearing at most playback levels. This jitter‐induced distortion is loud enough to be heard whenever it is not masked by musical content.
Killing Jitter
Phase Locked Loop (PLL) circuits are used to filter clock signals. A PLL is an electronic equivalent to a flywheel. Prior to the CD, cheap record players were abundant. These often had lightweight stamped metal platters. In contrast, high‐end turntables have massive platters to help them spin at a constant rate. A PLL stores and releases electrical energy in much the same way as a flywheel stores and releases mechanical energy. Some turntables have heavy flywheels, others do not. Likewise, some PLLs have a slow enough response, and enough inertia to adequately remove jitter, others do not. We can look at a turntable and see the size of the flywheel, but we can’t look at a digital converter and see the size of the “electronic flywheel” contained in the PLL circuit. Jitter attenuation specifications are essential for assessing the effectiveness of the PLL.
“Jitter‐Free” Playback is Possible
The Benchmark DAC1 and ADC1 converters have enough jitter attenuation to ensure jitter that measures less than +/‐ 7 psec (+/‐ 7 trillionth of a second) under all input conditions. These products maintain jitter‐induced distortion at levels that are at least 130 dB below the peak level of the music. This distortion is well below the threshold of hearing (at any reasonable playback level). The Benchmark DAC1 and ADC1 converters will not add audible jitter artifacts under any operating conditions. With these converters, jitter is so far below audibility that these devices can essentially be considered “jitter free”.
Jitter in Recordings Cannot be Removed
Unfortunately, many digital recordings (especially older recordings) were made with converters that had significant jitter problems. No D/A converter can remove the jitter-induced artifacts encoded into a recording by a poor‐quality A/D converter. In the future it may be possible to remove some encoded jitter using digital signal processing (DSP), but nothing of this sort is currently available. A good D/A converter can only guarantee that no additional jitter artifacts are added.
“Evil” #2 - Quantization Errors
All digital systems “quantize” an analog signal into a limited number of digital codes. “Quantization” is essentially a numeric rounding process. The accuracy of any number is reduced when rounding is applied. For example, the numbers 4.2 and 4.4 can both be rounded to 4. The rounding caused errors of 0.2 and 0.4 respectively. Similarly, the instantaneous voltage of an analog signal could be modeled as an integer followed by a nearly‐infinite number of decimal places. Quantization would be analogous to rounding this exact quantity to the nearest integer.
The accuracy of any analog signal is reduced when quantization is applied. The quantization process adds errors to the audio. The magnitude and character of these errors can vary significantly depending upon system design. In a poorly designed system, quantization errors can take the form of a very non‐musical and distorted version of the input audio. In a well‐designed system, these quantization errors can take the form of white‐noise, can be held to inaudible levels, and can be moved to inaudible frequencies.
We will look at how we can achieve distortion‐free quantization, and then we will look at how quantization noise can be reduced to levels that are well below audibility. We will also show how digital systems can be modified to accurately resolve signals that have amplitudes much smaller than one quantization level.
Staircase Analogy
The classic analogy for a digital system is a staircase. Each step represents one unique digital code or “quantization level”. A 16‐bit system has 2^16 unique digital codes. Our 16‐bit staircase has 65,536 steps. With so many steps, how important is any one single step? The answer is 1 out of 65,536. If we do the math, this is 0.0015%. If we want to express this in dB, this is given by 20*Log(1/65,536) = ‐96 dB. An error of one step creates distortion at a level that is 96 dB below the peak levels that can be represented in a 16‐bit system.
If the volume of the playback system is adjusted so that peak playback levels exceed 96 dB SPL, these ‐96 dB errors will exceed the threshold of hearing. These errors are ‐96 dB relative to the peak level that can be represented by the 16‐bit digital system. They are not necessarily ‐96 dB relative to the level of the music! Peak levels are often 18 dB higher than average levels. In a 16‐bit system, these quantization errors may be only 78 dB (96‐18=78) below the average level of a loud passage of music. What is worse is that these quantization errors may exceed the level of the music being played during low-level passages. Audio often fades at the end of an audio track. Near the end of these fades, quantization errors can easily exceed the level of the music! Quantization errors can be a serious problem in a 16‐bit audio system.
Staircase, Hill, and Laser Pointer – A walk inside of an A/D converter
To understand quantization errors, let’s imagine that I have a hill facing the staircase. For simplicity, let’s just say that the steps are all 1 foot high. I paint a number on each step riser to identify each step. The hill facing the staircase is analog – it has no steps. I can walk up and down the hill and stop anywhere I like. If I carry a laser pointer, hold it level, and point it at the staircase, my movements up and down the hill will be quantized by the staircase riser number illuminated by my laser. I will have created a giant A/D converter. I decide to test my new digital system:
If I start at the bottom of the hill and climb 10 feet, my laser pointer says I have reached step riser 10. If I climb another 5 feet, it says I have reached step riser 15 – all is good. Now, let’s suppose I climb another ½ foot. My laser is still pointing to step riser 15. According to the numbering on the risers, I have not moved. I am still on step riser 15! My A/D converter ignored my ½ foot movement. I can move back down ½ foot and back up ½ foot and my A/D will completely ignore my movements. Movements as large as almost 1 foot up and then back down are completely ignored. Obviously my A/D converter has a problem – it can ignore small movements. Now let’s assume I start 15 feet up the analog hill and then move down ½ foot. My laser is now pointing to step riser 14. My A/D converter now says that I have moved 1 foot (from 15 to 14). In reality, I only moved ½ foot. I then discover that very small movements around the 15 foot elevation produce a change of 1 on my staircase. Again my A/D converter has a problem – it can amplify small movements. The first ½ step up from 15 was ignored (or muted) while the ½ step down from 15 was amplified.
Quantization errors can mute audio details, or amplify audio details. For this reason, quantization errors can add very high distortion to low‐level signals. Reverberation tails, and low‐level passages of music are most vulnerable to quantization distortion.
Frustrated with the poor performance of my hill‐side A/D converter, I take a long coffee break...
Too Many Cups of Coffee – A solution to the quantization distortion problem
After far too many cups of coffee, I venture back to my hill‐side A/D. I repeat my movements from the first test, but now I am getting different results! My initial climb of 10 feet should have landed my laser on step riser 10. Instead it is randomly hitting riser 9 and 10. Half of the time it hits 9 and half of the time it hits 10. Clearly the coffee has impaired my ability to hold the laser steady. I move ½ foot up the hill and my laser now points to 10 much more often than 9. I experiment a little and discover that very small movements on the analog hill produce changes in the distribution of numbers quantized by the steps. If I average the results, I find that my digital system knows exactly where I am on the analog hillside. The random movements of my hand “dither” the position of the laser pointer. Dither is a random noise that is added to digital systems in order to eliminate quantization distortion. When dither is applied, the quantization noise still remains, but the distortion is gone.
Killing Quantization Distortion with Dither – Musical Details are Saved
When properly dithered, digital systems behave exactly like analog systems: The low-level resolution of a properly‐dithered digital system is only limited by noise. No quantization distortion is present when a digital system is properly dithered. It is a common misconception that a 16‐bit system is deaf to signals that are more than 96 dB below full scale. A 16‐bit system that is properly dithered with white‐noise dither can just sound like an analog system having a 93 dB signal to noise ratio. The white‐noise dither adds some noise reducing the signal‐to‐noise ratio (SNR) to 93 dB, but this dither entirely eliminates the quantization distortion. It can be shown mathematically that a properly‐dithered digital system has the same resolution as an analog system having the same signal to noise ratio. Our ears have an amazing ability to hear sounds that are as much as 30 dB lower in amplitude than the noise around us. If we are listening to a properly‐dithered 16‐bit system, it is possible to hear musical tones that are 30 dB lower than the noise (or 30+93=123 dB below full scale). Low‐level tones are digitized and reproduced without quantization distortion. Once a digital system is properly dithered, we can focus our efforts on improving signal‐to‐noise ratios. Dither does not remove quantization noise, but it can remove all of the quantization distortion. Dither does not mask (or cover up) the quantization distortion, it actually eliminates the distortion by converting it to random noise.
Killing Quantization Noise with More Bits
Clearly, if we throw enough bits at the quantization “evil” we will have victory. 16, 24, 32, do I hear 64? Where do we stop? Analog seems to have an infinite number of bits. The truth is that all analog electronic systems are quantized by electrons, but this is a topic for another time and place.
A 16‐bit system has 2^16 or 65,536 levels available for quantizing a signal. A 24‐bit system has 2^24 or 16,777,216 levels available. It is easy to see why a 24‐bit signal should have advantages over a 16‐bit system. The 24‐bit “staircase” has 16 steps for every step on our 16‐bit “staircase”. Obviously accuracy should improve. If we do the math, we see that the error in a 24‐bit system is 1/16,777,216 = 0.000006%. Expressed in dB the error signal is 20*Log(1/16,777,216)=‐144 dB (relative to the maximum output level). Errors that are 144 dB below peak level are well below the threshold of hearing, even at very loud listening levels. Adding bits can reduce quantization errors to insignificant levels. Every additional bit reduces the error level (distortion or noise) by 6 dB.
Imagine how bad things would be if we only had a 1‐bit digital system! But wait …
Killing Quantization Noise with High Sample Rates
Sony’s DSD (SACD) system is a 1‐bit system and only has 2 quantization levels available. It has a quantization noise level of 20*Log(1/2)=‐6dB. A DSD system only has a 6 dB dynamic range when measured over its entire bandwidth! How does this even work? Or, why does it work so well?
Sony chose to throw high sample rates at the problem, and they showed that a high-quality digital system could be built around a 1‐bit format. Actually this was nothing new; 1‐bit A/D and D/A converters were readily available when DSD was proposed. Sony simply suggested that we connect our 1‐bit A/D converters directly to our 1‐bit D/A converters to reduce the system processing.
A 1‐bit Digital Experiment – try this at home
If you are fortunate enough to have at least one old‐fashioned tungsten light bulb in your house, try this: Walk over to the light switch and try dimming light by rapidly turning the switch on and off. If you are really clever (and fast) you can actually adjust the brightness of the light by varying the time spent in the on position. If the switching is fast enough, the light will cease to flicker. The now‐illegal mercury‐wetted “silent switches” are ideal for these experiments. Any brightness between full off and full on can be achieved with only 1‐bit (a single switch). I suspect many of us experimented with 1‐bit digital systems as children but were scolded for playing with the lights. I even recall watching my father replace a light switch that mysteriously failed after some extended 1‐bit experiments.
Most light dimmers actually control brightness by turning the lights on and off 120 times per second (100 times per second if you have 50 Hz power). We can’t see the flicker, but sometimes it is possible to hear the filament of the bulb vibrate when dimmed to low brightness. The 1‐bit quantization noise of the light dimmer is at too high a frequency to see (120 Hz), but it can be heard. The vibrating filament confirms that the quantization noise is present, even though our eyes cannot see any flickering. The light dimmer hides the 1‐bit quantization noise by operating at a 120 Hz switching frequency. Some of the flickering is removed by the thermal inertia of the filament, and some is removed by the slow temporal response of our eyes.
Sony’s DSD Systems Hides Quantization Noise at Ultrasonic Frequencies
DSD audio systems hide 1‐bit quantization noise by toggling at 2.8224 MHz. Most of the quantization noise in a 1‐bit DSD system is above 20 kHz so we are not able to hear it. Some of the DSD quantization noise is removed by analog lowpass filters, and some is removed by the limited frequency response of our ears. DSD operates at a sample rate of 2.8224 MHz (64 x 44.1 kHz). This means that the quantization noise in DSD can be spread across a bandwidth that is 64 times as wide as a conventional 44.1 kHz PCM system. The quantization noise is “hidden” at frequencies that we cannot hear, and at frequencies that cannot be reproduced by our playback system.
High Sample Rates Provide More Space to Hide Quantization Noise
If quantization noise is evenly distributed across the bandwidth of a system, every
doubling of bandwidth reduces the noise in the audio band by 6dB. DSD doubles the bandwidth of a CD 6 times to achieve a bandwidth that is 64 times as wide. At 6dB per doubling, DSD achieves a 36 dB reduction of in‐band quantization noise. By itself, this added improvement would still only give DSD a SNR of 42 dB (6 dB + 36 dB). DSD systems must make heavy use of a technique known as “noise shaping” to move much more of the quantization noise to ultrasonic frequencies where it cannot be heard.
Noise Shaping – If you can’t get rid of the noise, just hide it!
Noise shaping is sort of like cleaning house. If you aren’t ready to throw the junk out, just move it out of the way ‐ put it in the attic where it cannot be seen. DSD has a huge “attic” where quantization noise can be hidden. DSD’s “attic” begins at 20 kHz and extends up to 1411.2 kHz. To achieve acceptable signal to noise ratios in a 1‐bit DSD system, aggressive noise shaping is used to move the quantization noise out of the audio band and into ultrasonic frequencies. The result is that a 1‐bit DSD system can have a 120 dB or better SNR when measured over a 20 kHz bandwidth. On playback, the ultrasonic noise can be removed with an analog low‐pass filter (at the output of the D/A converter). After filtering, the resulting signal will be free from any apparent quantization errors. DSD proves that a 1‐bit system with aggressive noise shaping and a very high sample rate, can rival a 96 kHz 20‐bit PCM system.
Noise Shaping Has Improved the Quality of 16‐bit CD’s
Noise shaping is now almost always used to master 16‐bit CD’s. This noise shaping is not as effective as the noise shaping in a DSD system. CD’s are restricted to a 44.1 kHz sample rate and therefore they have a very small “attic” in which to hide junk. Noise must be moved into the rather narrow region between 18 kHz and 22 kHz. CD’s have a 4 kHz band in which to hide noise. In contrast, DSD has over 1300 kHz available to hide noise, but DSD has a lot more quantization noise to hide. The bottom line is that a noise shaped 16‐bit CD system can rival the performance of a 44.1 kHz 20‐bit system that lacks noise‐shaping. Properly dithered and noise‐shaped CD recordings have the ability
to audibly reproduce tones that are in excess of 140 dB below full scale. Because of the noise shaping, these 16‐bit recordings can sound like they have a 120 dB SNR. In most cases, the noise from microphones, analog electronics, and studios, greatly exceed the perceived noise of a noise‐shaped 16‐bit system. Based on signal to noise consideration, a 16‐bit 44.1 kHz system should be capable of delivering extremely high quality audio. If you have any doubts about the effectiveness of dither and noise shaping, remember that DSD only has one bit.
A Better Solution – Increase Both the Sample Rate and the Bit Depth
Combining 96 kHz with 24 bits yields an in‐band SNR of over 150 dB! The quantization noise in a 96 kHz 24‐bit system is well below audible levels at even the loudest playback levels. 96/24 systems do not need noise shaping, nor do they need analog lowpass filters to remove ultrasonic noise. The 24‐bit word length makes digital processing simple and transparent. It is therefore an ideal format for recording, editing, and mixing. 16‐bit systems degrade quickly when processed. 1‐bit DSD systems are extremely difficult to process. The quality of a DSD recording can degrade very quickly when mixing and editing. Benchmark does not recommend CD or DSD systems for professional recording, editing, and mixing applications. In our opinion, these formats are only suitable for distribution of the final product.
1‐bit Works, 16‐bits Work, Why 24?
OK, if dither and noise shaping work so well, why do we have 24‐bit audio systems? Are the extra bits just marketing hype? Are we buying something that we do not need? The answer is a definite no!
Until a few years ago, most digital audio was recorded, edited, mixed, and mastered in 16‐bits. Unfortunately, digital audio degrades very quickly when subjected to 16‐bit mathematical operations. The problem with this is that every mathematical process applied to the 16‐bit audio creates a result that has more than 16‐bits.
To understand how this works, let’s consider an example: Suppose I put a dollar in a savings account. If the dollar earns 1% interest I now have $1.01. If I then earn 1% on my $1.01, I now have $1.0201 until my bank rounds this down to $1.02. Money is lost in my bank account due to rounding, and in the same way, audio detail can be lost in an audio DSP system.
DSP operations extend word lengths. If these extended word lengths are truncated or rounded back to their original length, we introduced another quantization process. Like the quantization process in an A/D converter, this quantization process can be dithered, and noise shaped to reduce its audibility. Nevertheless, noise will rise with every requantization. If dither is omitted, distortion will rise quickly with every operation.
The earliest CDs were mixed and mastered with analog equipment. The transfer to digital, involved a single 16-bit A/D conversion. At that time, the A/D converters were a weak link. As A/D converters improved, so did CDs. This improvement came to a screeching halt in the early 1990's when 16-bit digital mixers, digital recorders, and digital audio workstations were introduced. These early digital systems operated at 16‐bits, used 16-bit math, and lacked dither. These systems streamlined the production process, and eliminated analog tape, but produced some of the worst sounding digital artifacts. These early digital systems may be largely responsible for digital audio’s bad reputation. These recordings clearly demonstrate the need for higher resolutions in the studio.
24‐bit systems were rare until the late 1990's. Pro Tools introduced their 24-bit system in 1997, and within a few years, many studios upgraded to these vastly improved digital platforms. 24‐bit audio is very robust when passed through cascaded digital processes. In contrast, 16‐bit audio is very fragile and it degrades quickly when DSP processing stages are cascaded.
Every added bit reduces the damage done per DSP operation by 6 dB. It takes 256 DSP operations at 24‐bits to equal the damage done by one 16‐bit DSP operation. Many high‐quality professional mixing, editing, and effects systems now use 32‐bit DSP internal processing to ensure that any errors are well below audibility.
“Evil” #3 - Aliasing
Aliasing is an effect that frequency‐shifts signals so that they are incorrectly represented. In digital audio systems, ultrasonic tones may be aliased such that they are reproduced at audible frequencies. This frequency shifting may also reverse the relative locations of tones within a multi‐tone signal such that a higher tone is reproduced below a lower tone. Alias tones produced from inaudible ultrasonic tones can clutter the audible band with tones that have no relationship to the music. The destructive effects of aliasing raise havoc on a musical signal. What causes aliasing? Is there a cure?
Wagon Wheels and Old Movies ‐ A Foreshadowing of Future Problems
The wagon wheels in old western movies often seemed to turn backward. As a wagon began to move, the wheels would appear to begin turning in the forward direction, but then they would appear to slow, then stop, and then reverse as the wagon gained speed. In some cases it was possible to see the wheels reverse several times as the wagon accelerated. Was something wrong with the old wagons, or was something wrong with our movie equipment? The answer of course is that wagons are wagons, but movies are flicks. Movie cameras capture 24 still images (or frames) per second, and projectors flash 24 still images before our eyes each second. This flickering of still images gives movies their nickname (flicks).
When the images flash fast enough, we correctly perceive the motion in the images. If the spokes of the wagon wheel move less than ½ spoke position from one image to the next, we can accurately interpret the speed and direction of the wheel. If the wheel turns exactly one ½ spoke position the direction of motion of the wheel cannot be determined. It could be rotating forward or backward by ½ spoke position per frame. If the wheel moves more than ½ spoke position but less than 1 spoke position between successive images, the wheel would appear to rotate backward. As the rotational speed of the wheel increases, the perceived direction of rotation will keep changing until each image becomes sufficiently blurred such that the spokes are no longer visible.
Like Movies, Digital Audio Systems can have Aliasing Problems
Movies are sampled systems. Images are samples 24 times per second in an effort to capture motion. Similarly, digital CD systems sample music at a much faster 44,100 times per second in an effort to capture the waveform of the music.
If a wagon wheel moves less than one‐half spoke between frames, its motion is preserved. If an audio signal changes less than one‐half cycle between samples, its “motion” is preserved. For this reason, a digital system that samples at 44.1 kHz can only accurately reproduce audio signals having a frequency less than 22.05 kHz (one half of the sampling rate – also known as the Nyquist frequency).
Tones between 22.05 kHz and 44.1 kHz will “alias” down to lower frequencies (much like the wagon wheel appeared to turn backward). Tones at exactly 44.1 kHz will disappear (much like the wagon wheel appeared to stop at a rotation rate of one spoke per frame). A 44,000 Hz input tone will alias to 100 Hz (44,100 – 44,000). A 43,900 Hz tone will alias to 200 Hz (44,100 – 43,900). A 22,150 Hz tone will alias to 19,950 (44,100 – 22,150).
Attempting to Kill Aliasing with High Sample Rates
If we were to speed up the frame rate of movies, they could capture a wider range of rotational speeds without aliasing. Similarly, 96 kHz, 192 kHz or even 2.8224 MHz audio systems can accurately represent a wider range of frequencies than the 44.1 kHz CD system. Nevertheless, aliasing will still occur whenever that audio input frequency exceeds one half of the sampling frequency. A high sample rate cannot guarantee that aliasing will not occur.
Killing Aliasing with Low‐Pass Filters
Aliasing will not occur if we remove high‐frequency signals before they are sampled. In the example of the movie, aliasing stops when the motion is so fast that the spokes are blurred to the extent that they are no longer visible. The open shutter of a camera creates a low‐pass filter that blurs motion. If the blurring is sufficient, aliasing is prevented.
In a CD system, we must filter out all signals above 22.050 kHz while attempting to leave audible frequencies untouched. We would like to pass 20 kHz without loss while removing 22 kHz. This is a very difficult task, and it requires a very abrupt low‐pass filter. In the early days of digital audio, these “brick‐wall” filters were analog filters. Unfortunately, it is very difficult to build analog filters that have the necessary performance. Consequently, many early recording and playback systems suffered from some audible aliasing problems, and/or some loss of frequency response.
It is much easier to construct a brick‐wall digital anti‐alias filter. Converters can be configured to “oversample” at some multiple of the desired sample rate. A brick‐wall digital filter can be applied when the audio is down‐sampled to the desired output sample rate. A very simple analog low‐pass filter must still be used to remove very high frequency signals from the input of the oversampled converter. Virtually all digital audio systems now use over sampled A/D and D/A converter. Aliasing is rarely a problem in these newer “oversampled” audio converters.
Low‐pass filters are applied in the A/D to prevent aliasing. Low‐pass filters are applied in D/A converters to remove sampling artifacts and produce a continuous waveform that has no evidence of passing through a sampled system. End‐to‐end, a digital audio system can be indistinguishable from a band‐limited analog system.
In Summary
Quantization
Quantization distortion can be completely eliminated with dither. The number of bits, the sample rate, and the type of dither employed will collectively determine the SNR of the digital transmission system.
Jitter
Jitter‐induced distortion can be reduced to levels that are well below audibility. Many newer recordings are essentially jitter‐free. If reproduced through a low‐jitter D/A converter, jitter‐induced distortion will not even approach audibility.
Aliasing
Aliasing has been virtually eliminated through the use of oversampled converters. No audible aliasing artifacts should exist in a well‐designed 44.1 kHz system.
Limits of the CD
The audio industry has produced thousands of CD titles that include all 3 of the “digital evils” at audible levels. These older recordings do not accurately represent the capabilities of the CD system. Clearly the CD format has not delivered “perfect audio forever”, but it can now deliver “nearly perfect audio”. We haven’t followed the wrong path for 28 years; it has just taken us that long to perfect the system. Few commercial recordings reach the performance that is achievable with the CD format. For this reason, 44.1 kHz 16‐bit systems still remain a viable distribution format for high‐quality recordings. While the CD format is well‐suited for distribution of the finished product, Benchmark does not recommend this format for recording or production use as the quality degrades rapidly when processing is applied.
DSD (1-bit Digital Systems)
In theory, the DSD system can offer a slightly better signal to noise ratio than a noise-shaped CD system. It can also provide a slightly wider usable bandwidth. Unfortunately, neither of these capabilities may be realized in a recording that was completely recorded and produced in DSD.
DSD relies on very aggressive use of noise shaping, and consequently, it is even less robust than the CD format in a production environment. DSD 1‐bit signals are not easy to process and quality can degrade quickly in mixing and mastering operations. For these reasons, Benchmark does not recommend DSD for production use. We believe that DSD recordings usually fail to deliver the benefits claimed for the format.
High-Resolution PCM
High‐resolution 96 kHz 24‐bit systems are essentially artifact‐free when properly designed. All distortion and noise artifacts can be held well below audibility in these systems. These high‐resolution digital systems can capture, store, process, and reproduce analog signals without a hint of quantization, jitter, or aliasing. These systems have sufficient resolution to tolerate many stages of digital processing and are ideally suited for recording, production, and distribution.
Leave a comment
Comments will be approved before showing up.
Also in Audio Application Notes

How Loud is the Distortion from Your Power Amplifier?
by John Siau August 08, 2025
Would you put a Washing Machine in your Listening Room?
If the answer is no, you may be surprised to discover that the distortion produced by your power amplifier may be louder than the noise produced by a major appliance.
Don't believe me? Take a look at Stereophile's test reports:
We selected 7 power amplifiers from Stereophile's top list of recommended amplifiers.
We took Stereophile's "THD+N vs. Power" plots for each, and replotted the data in a format that shows the loudness of the THD+N at the listening position.
The results are shocking!
Amplifier THD+N is louder than expected!
The distortion from your amplifier may be louder than a washing machine on the spin cycle, or it may be totally silent. How does yours perform? The answer is hidden in Stereophile's THD+N plots.
This application note reveals the hidden truth:
"The Distortion from your Power Amplifier may be Louder than a Washing Machine!"
I know, it sounds crazy, but this is what the measurements show!
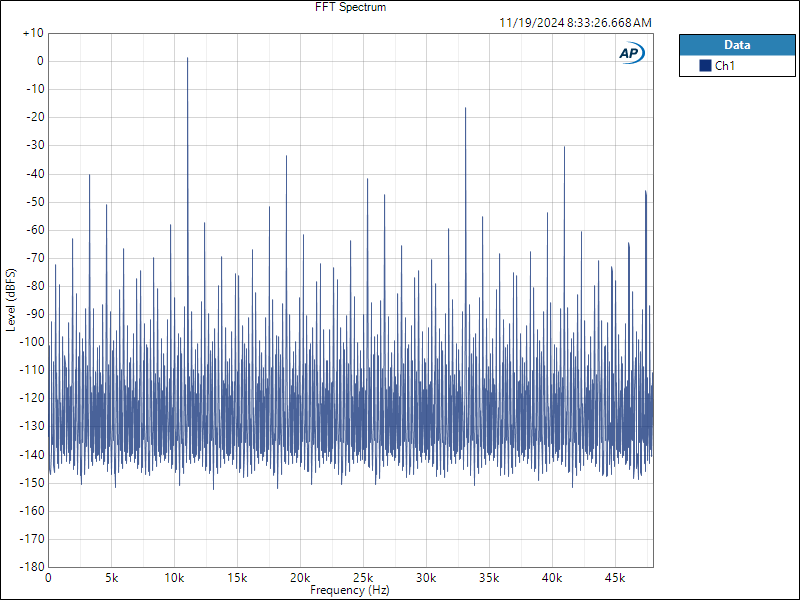
Interpolator Overload Distortion
by John Siau November 20, 2024
Most digital playback devices include digital interpolators. These interpolators increase the sample rate of the incoming audio to improve the performance of the playback system. Interpolators are essential in oversampled sigma-delta D/A converters, and in sample rate converters. In general, interpolators have vastly improved the performance of audio D/A converters by eliminating the need for analog brick wall filters. Nevertheless, digital interpolators have brick wall digital filters that can produce unique distortion signatures when they are overloaded.
10% Distortion
An interpolator that performs wonderfully when tested with standard test tones, may overload severely when playing the inter-sample musical peaks that are captured on a typical CD. In our tests, we observed THD+N levels exceeding 10% while interpolator overloads were occurring. The highest levels were produced by devices that included ASRC sample rate converters.

Audiophile Snake Oil
by John Siau April 05, 2024
The Audiophile Wild West
Audiophiles live in the wild west. $495 will buy an "audiophile fuse" to replace the $1 generic fuse that came in your audio amplifier. $10,000 will buy a set of "audiophile speaker cables" to replace the $20 wires you purchased at the local hardware store. We are told that these $10,000 cables can be improved if we add a set of $300 "cable elevators" to dampen vibrations. You didn't even know that you needed elevators! And let's not forget to budget at least $200 for each of the "isolation platforms" we will need under our electronic components. Furthermore, it seems that any so-called "audiophile power cord" that costs less than $100, does not belong in a high-end system. And, if cost is no object, there are premium versions of each that can be purchased by the most discerning customers. A top-of-the line power cord could run $5000. One magazine claims that "the majority of listeners were able to hear the difference between a $5 power cable and a $5,000 power cord". Can you hear the difference? If not, are you really an audiophile?

