Buy one component and save 10% on up to 2 cables. Buy 2 components and get 4 free cables. Free shipping on USA orders over $700.
Buy one component and save 10% on up to 2 cables. Buy 2 components and get 4 free cables. Free shipping on USA orders over $700.
High-Resolution Audio - Sample Rate
by John Siau March 19, 2015

Digital recordings are now available in a variety of sample rates. The CD uses a 44.1 kHz sample rate, but high-resolution audio recordings are now available in sample rates of 96 kHz and 192 kHz. What are the advantages of higher sample rates? How high a sample rate do we really need?
Digital audio systems take instantaneous snapshots or "samples" of an analog audio signal and then store each of these samples as numeric values. The digital samples can be stored and transmitted without any loss of quality, but these samples must be used to reconstruct an analog signal before we can listen to the audio. The sample rate places very specific limitations on the quality of the audio that can be transmitted through the digital system. It is important to understand these limitations so that we can make intelligent decisions when selecting recording and playback formats. The absolute high-frequency limit of a digital system is 1/2 of the sample rate. Many people are familiar with this limit, but they question the ability of the digital system to sample, transmit, and reconstruct frequencies below this upper limit. It is important to separate myth from facts in order to gain a clear picture of how sampling works.

Sampling the Speed of a Runner
Every timed athletic race uses sampling to determine speed. Imagine a 1 mile race on a 1/4 mile track. We need to take just two samples in order to determine the average speed of the runner over the course of the race. To do this, we take a time sample at the beginning of the race and a time sample at the end of the race (we start the clock and stop the clock). If the time difference between the two samples is 4 minutes, then our runner has completed his 1 mile race in 4 minutes. This means that our runner achieved an average speed of 15 MPH over the duration of the race. With only two samples, we can determine his average speed, but we don't know how fast he ran on each of the four laps.
If we want more information, we need more samples. If we record the runner's time at the completion of each lap, we now know his average speed for each lap. But, for a given lap, we still don't know which half of the lap he ran faster. Again, we need more samples if we want more information.
We can divide the track in half and double the number of time samples we are recording. If we still want more information, we can divide the track in two again and record 1/4-lap times. If this still isn't enough information, we can put more marks on the track and take more samples. But, at some point, the additional information becomes useless.
When the marks get very close together, the runner's change in speed between one set of marks and the next may be so small that the change in speed is meaningless. We have reached the point where additional time samples will not give us any meaningful new information. At this point, we would have enough information to accurately determine the runner's time to reach any arbitrary position between marks. No additional information would be gained by adding more marks to the track to sample the runner's position.
The High-Resolution Audio Race
The audio industry has been in a race to double and quadruple the sample rate of the CD. More samples will provide more information, but when do we reach the point when no meaningful information is gained? We have doubled and quadrupled the sample rate of the CD. Have we reached the point where additional samples are meaningless, or do we still need higher sample rates? What are the advantages of a higher sample rate?
To answer these questions, let's look at another simple sampling system:

Sampling the Speed of a Rotating Wheel
If we point a video camera at a slowly rotating wheel, we can take snapshots of the position of the wheel and determine the rotational speed of the wheel. If we use a video camera that takes 30 snapshots (video frames) every second, then we will have 30 samples per second (a sample rate of 30 Hz). We can look at two successive snapshots and see how far the wheel has rotated in 1/30th of a second.
If we see that it rotated 1/4 of a revolution in 1/30th of a second, we can do the math and determine that the average speed between those two samples was 7.5 revolutions per second (or 450 RPM). By looking at just these two snapshots, we can also determine which direction the wheel was rotating. From only two snapshots, we know the position, the average speed, and the direction of rotation. We also have a pretty good idea where it will be in the next snapshot. This is a lot of information, and it is provided by only two samples!
A Perfect Time Machine
If the wheel is rotating at a nearly constant rate, we can make very accurate predictions about where we can expect it to be in future snapshots. We can even estimate the position of the wheel at any point in time between snapshots.
If the rotational speed is perfectly constant, we would have infinite time resolution, and we could determine the exact position of the wheel at any arbitrary point in the past, present or future. We could even create an image showing how the wheel would look at any arbitrary point in time. This process of creating new images between samples is known as interpolation and it is an important part of reconstructing continuous motion from a series of discrete samples. Our interpolation will be perfect if the rotational speed of the wheel is perfectly constant. Under these conditions, we would have the perfect time machine!
A Near-Perfect Time Machine
In the real world nothing is ever perfectly constant, and the speed of our wheel will change over time. Nevertheless, we will always know the exact position of the wheel at each of our snapshot samples. This means that we can always accurately interpolate the position of the wheel just before or after a sample.
As we move away from a sample we know less about the position of the wheel and our interpolation errors will increase. We will have the highest errors when we attempt to interpolate the position of the wheel at a point in time that is half way between two successive samples. These errors would be reduced if the time between samples was reduced. Interpolation errors are reduced when sample rates are increased.
If the speed of the wheel changes gradually, the errors will be small, and our "time machine" will work well. If the speed of the wheel changes very little between successive samples, we can interpolate the position very accurately at any point between the samples. Interpolation errors are small when conditions change slowly relative to the sample rate.
Interpolation is an important part of reconstructing continuous motion from a series of still snapshots. The sample rate must be high enough to allow accurate interpolation, but at some point, the improvement becomes insignificant.
Again we ask; how fast do we need to sample?
Turning the Wheel Backward
A big problem can occur with our wheel and camera system if we try to spin the wheel too fast. We have all seen movies or videos where a wheel appears to stand still, turn backward, or turn at the wrong speed. These gross errors occur when we are not taking snapshots of the wheel fast enough.
Let's spin our wheel quickly and see what happens:
If we spin our wheel at exactly one revolution every 1/30th of a second, while taking snapshots once every 1/30th of a second, the wheel will rotate exactly once between successive samples. This means that every image in our video will be identical. The wheel will appear stationary in our video, yet it is rotating at a rate of 30 revolutions per second.
If we slow the wheel slightly, it will make slightly less than one revolution between video frames and each successive snapshot will show the wheel at a position that is slightly earlier in the rotation. This means that when we play our video, the wheel will now appear to turn backward at a slow rate! The apparent direction is wrong, and the apparent speed is wrong!
If we slow our wheel some more so that it makes exactly 3/4 of a revolution between successive samples, it will appear to move backward at a rate of 1/4 revolution per sample, or 7.5 revolutions per second. The actual speed is 3/4 revolution in 1/30th of a second or 22.5 revolutions per second. Again, the apparent speed is wrong and the apparent direction is wrong!
Notice that as we slowed the wheel down it appeared to move faster. Our sampled system is clearly not working properly when the wheel is rotating this fast, but it was working well when the wheel was rotating slowly.
How slow does the wheel have to turn to look right in our video?
Finding the Limit
We will continue to slow the wheel until our wheel and camera sampling system starts to work properly. As we slow the wheel, it continues to appear to move at a faster and faster rate, but still in the wrong direction.
If we slow the wheel to exactly 1/2 revolution between successive samples, a strange thing happens. We suddenly lose our sense of which direction the wheel is rotating. To understand this, imagine that the first sample captures the wheel at a 12:00 position. The next sample will happen 1/2 revolution later, and the next video frame will capture the wheel at a 6:00 position. The 3rd frame will show the wheel back at its original 12:00 position. Successive frames will simply show the wheel alternating between the 6:00 and 12:00 positions. Under these circumstances we will lose all sense of which direction the wheel is rotating. Our video frames clearly imply that the wheel rotates exactly 1/2 revolution between frames. The apparent rotational rate is correct, but there is no information in the snapshots that will tell us which way the wheel is rotating (assuming our snapshots are instantaneous and free from any blurring).
At 1/2 rotation per frame, our wheel and camera system is almost working; we are sensing speed but not direction. At this speed we have exactly two samples (video frames) per rotation of the wheel. The wheel is rotating at 15 revolutions per second (15 Hz) and the camera is sampling at 30 frames per second (30 Hz). The sample frequency is exactly twice the rotational frequency of the wheel.
If we slow the wheel to a rate just below 1/2 revolution per video frame, the images no longer alternate between the 12:00 and 6:00 positions. Each successive image shows just less than 1/2 rotation. The images clearly show that the wheel is rotating. The apparent rate and apparent direction are both correct, and we can estimate where the wheel will be at any arbitrary point in time. Our camera and wheel system start to work when we have just slightly more than 2 samples per rotation of the wheel.
The Nyquist Limit
The relationship that we have found is known as the Nyquist limit. Digital systems must take more than 2 samples per cycle of a signal in order to correctly determine the frequency and phase rotation of the signal. If this condition is satisfied we can interpolate to recover the position of the signal at any arbitrary points in time between samples. A continuous signal can be correctly recovered from a series of samples if the Nyquist limit is satisfied.
Exceeding the Speed Limit
When the sample rate was too low in our wheel and camera system, we lost our sense of rotational direction and speed. What we saw was an "alias" of the true motion. A similar situation occurs if an audio A/D converter is sampling too slowly relative to the frequencies contained in the music. High frequency tones can be aliased to a different frequency and a tone that is rising in frequency can be aliased to a tone that is descending in frequency. If you are going to exceed the speed limit, use an alias when you get caught. This may be bad legal advice, but it may help you remember the importance of the Nyquist limit.
Back to Audio
It is often said that the upper limit of our hearing range is about 20 kHz. If we want to digitally record 20 kHz, the Nyquist limit tells us that we will need to use a sample rate that is higher than 40 kHz. This is one of the reasons that 44.1 kHz was selected as the sample rate for the CD.
At the CD sample rate of 44.1 kHz, audio frequencies below 22.05 kHz can be digitized, stored, and reconstructed into a continuous analog signal. Frequencies above 22.05 kHz will create alias tones that will contaminate the musical tones that are below 22.05 kHz.
Alias tones will only occur if frequencies above the Nyquist limit reach our A/D converter. To prevent this problem we insert low-pass filters that remove frequencies above 22.05 kHz. Ideally, we want to remove everything above 22.05 kHz while keeping everything that we can hear below 20 kHz. It turns out that this is a tall order. If we are not careful with our filter design, we may remove some of the audible frequencies, or leave some of the alias-producing frequencies.
In the early days of the CD format, steep analog filters were used at the input of A/D converters in order to reduce aliasing to an acceptable level. A few years later, we learned how to replace these analog filters with digital filters. A technique known as oversampling allows the use of digital filters that can have near-perfect rejection of alias-producing frequencies while preserving everything below 20 kHz.
Did this improvement finally allow the CD to give us "perfect sound forever"? This brings us to a set of "what if" questions:
What If
What if we can hear sounds a little higher than 20 kHz?
What if we can detect the presence or absence of overtones for a tone that is under 20 kHz? For example, can we tell the difference between an 8 kHz pure tone and an 8 kHz tone with a 24 kHz 3rd harmonic?
One thing is clear, the bandwidth of the CD format just barely exceeds 20 kHz. If 20 kHz is the true limit of our hearing, then the CD format is very efficient.
Data efficiency was very important when the CD was introduced in 1979. Data storage was expensive and it was important not to use a sample rate that was any higher than absolutely necessary. The 44.1 kHz sample rate allowed 74 minutes on a standard CD. A higher sample rate would have reduced the total play time. But, Norio Ohga, president of Sony, insisted that the CD must be able to record the longest known performance of Beethoven's 9th symphony. One performance of Beethoven's 9th, recorded in 1951, had a duration of 74 minutes, and the rest is history.
What if the conductor had moved his baton a little faster in 1951? Would we have a slightly higher sample rate on the CD? It is entirely possible!
What if Beethoven had written a shorter symphony in 1824?
It is hard to imagine that a piece of music recorded on paper in 1824, performed and recorded in 1951, played back and digitized in 1979, can be played back today on a system that was influenced by all of the participants.
Likewise, it is often hard to imagine how a continuous analog waveform can be sampled, stored, retrieved, and reconstructed into the original analog waveform. When this gets difficult, try to remember the runner and the rotating wheel. A few samples, or a few scribbles on a paper, can capture a lot of information, and it can be preserved for a very long time.
End of the "What If's"
The "what if's" all go away if we increase the sample rate. We probably would not need to increase the sample rate much beyond 44.1 kHz to capture every detail that we can hear. Video systems often use a slightly high 48 kHz sample rate for audio tracks. 48 kHz may be high enough to prevent audible defects, but it is still uncomfortably close to the limits of our hearing.
Jumping to an 88.2 kHz or 96 kHz (2X) sample rate should eliminate all concerns about exceeding the limits of our hearing. These systems provide a 44 kHz to 48 kHz upper limit on the frequency response. They also capture everything that we can capture with today's microphones. Furthermore, few loudspeaker transducers can reach these frequencies. With today's transducer technology, 2X sample rates are more than adequate. There is absolutely no advantage to sampling at 4X (176.4 kHz and 192 kHz) rates.
Transducers will improve, but human ears will stay the same. With improved transducers, the difference between 192 kHz and 96 kHz may be audible, but only because it makes the dogs bark. Anyone who claims otherwise may be barking up the wrong tree.
High-resolution releases are often different mixes than those released at 44.1 kHz. Be careful when attributing the difference to sample rate. 96 kHz may offer advantages when compared to 44.1 kHz, but there is no justification for paying a premium price to move from 96 kHz to 192 kHz, unless you are getting a better mix, better transfer, or better master.
Leave a comment
Comments will be approved before showing up.
Also in Audio Application Notes

How Loud is the Distortion from Your Power Amplifier?
by John Siau August 08, 2025
Would you put a Washing Machine in your Listening Room?
If the answer is no, you may be surprised to discover that the distortion produced by your power amplifier may be louder than the noise produced by a major appliance.
Don't believe me? Take a look at Stereophile's test reports:
We selected 7 power amplifiers from Stereophile's top list of recommended amplifiers.
We took Stereophile's "THD+N vs. Power" plots for each, and replotted the data in a format that shows the loudness of the THD+N at the listening position.
The results are shocking!
Amplifier THD+N is louder than expected!
The distortion from your amplifier may be louder than a washing machine on the spin cycle, or it may be totally silent. How does yours perform? The answer is hidden in Stereophile's THD+N plots.
This application note reveals the hidden truth:
"The Distortion from your Power Amplifier may be Louder than a Washing Machine!"
I know, it sounds crazy, but this is what the measurements show!
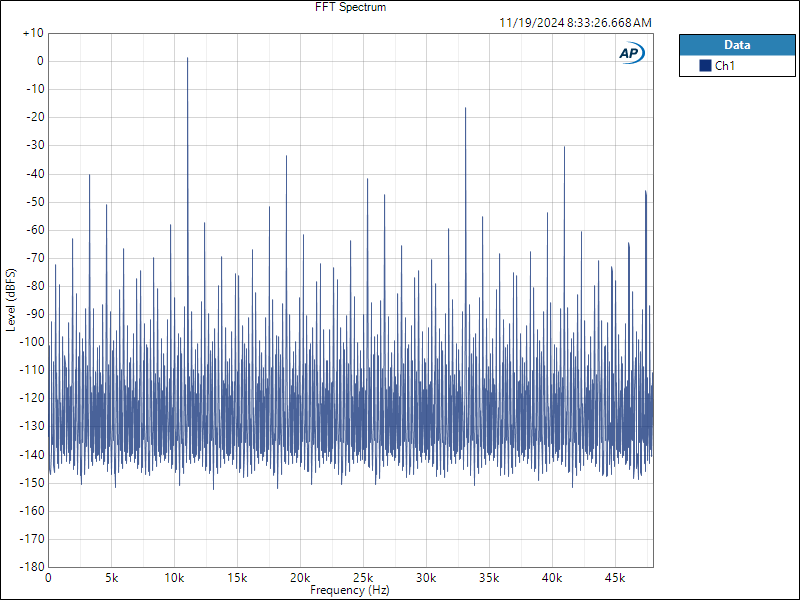
Interpolator Overload Distortion
by John Siau November 20, 2024
Most digital playback devices include digital interpolators. These interpolators increase the sample rate of the incoming audio to improve the performance of the playback system. Interpolators are essential in oversampled sigma-delta D/A converters, and in sample rate converters. In general, interpolators have vastly improved the performance of audio D/A converters by eliminating the need for analog brick wall filters. Nevertheless, digital interpolators have brick wall digital filters that can produce unique distortion signatures when they are overloaded.
10% Distortion
An interpolator that performs wonderfully when tested with standard test tones, may overload severely when playing the inter-sample musical peaks that are captured on a typical CD. In our tests, we observed THD+N levels exceeding 10% while interpolator overloads were occurring. The highest levels were produced by devices that included ASRC sample rate converters.

Audiophile Snake Oil
by John Siau April 05, 2024
The Audiophile Wild West
Audiophiles live in the wild west. $495 will buy an "audiophile fuse" to replace the $1 generic fuse that came in your audio amplifier. $10,000 will buy a set of "audiophile speaker cables" to replace the $20 wires you purchased at the local hardware store. We are told that these $10,000 cables can be improved if we add a set of $300 "cable elevators" to dampen vibrations. You didn't even know that you needed elevators! And let's not forget to budget at least $200 for each of the "isolation platforms" we will need under our electronic components. Furthermore, it seems that any so-called "audiophile power cord" that costs less than $100, does not belong in a high-end system. And, if cost is no object, there are premium versions of each that can be purchased by the most discerning customers. A top-of-the line power cord could run $5000. One magazine claims that "the majority of listeners were able to hear the difference between a $5 power cable and a $5,000 power cord". Can you hear the difference? If not, are you really an audiophile?

