Buy one component and save 10% on up to 2 cables. Buy 2 components and get 4 free cables. Free shipping on USA orders over $700.
Buy one component and save 10% on up to 2 cables. Buy 2 components and get 4 free cables. Free shipping on USA orders over $700.
Audio Myth - "24-bit Audio Has More Resolution Than 16-bit Audio"
by John Siau August 14, 2014
This myth goes something like this:
"Analog audio has infinite amplitude resolution."
"Digital audio is limited to a finite number of steps."
"24-bit audio has more resolution than 16-bit audio."
While it is true that digital systems quantize the amplitude of the audio signal to the nearest step in the digital encoding system, this does not necessarily mean that digital systems cannot have infinite resolution. Contrary to popular belief, digital systems can provide infinite amplitude resolution if they are properly dithered.
Dither Removes the Steps
Dither is a random noise signal that is added to the audio before it enters a digital quantizer such as an A/D converter. The dither signal places the quantization steps in random amplitudes relative to the audio signal. When this is done properly, the quantization errors produced by digital systems are nothing other than white noise. This means that an analog signal can be passed through a properly-dithered digital system (A/D - D/A) and then subtracted from itself producing a difference that is only random noise. This test is easy to perform in the lab and it absolutely confirms that digital systems can have infinite amplitude resolution.
I can hear the skeptics saying "this is wrong, 16-bit audio only gives you 65,536 discrete levels". Others are saying "24-bit audio gives you 16,777,216 discrete levels and this is much better than 16-bit audio". Others are saying "24-bits gives more resolution than 16-bits, so 32-bits would be even better". All are wrong! All have ignored the important role of dither in a digital system.
Some of you are still not buying this dither stuff, so I would like you to consider what happens when we reduce the number of bits. If a 16-bit system is "limited to 65,536 levels" an 8-bit system should be limited to 256 levels, and a 1-bit system should be limited to only 2 levels.
Let's examine what happens when we reduce the word length all the way to 1-bit:
DSD is a 1-bit PCM digital system. Nevertheless, is is obvious that DSD can resolve more than 2 discrete levels. The dynamics and character of the original performance can be digitized and transmitted through a 1-bit system! The continuous amplitude response of a DSD system is achieved through the use of dither and aggressive noise shaping. The noise shaping moves the dither noise and quantization noise out of the audible band and into ultrasonic frequencies. This gives 1-bit DSD a continuous amplitude response within the audible band. DSD provides proof that 1-bit systems can have an amplitude resolution that far exceeds the expected 2 quantization levels.
If a 1-bit system can provide a continuous amplitude response, it stands to reason that it should be much easier with 16-bits, and easier still with 24-bits.
If 1-bit systems work, is there any reason to use longer word lengths?
The only reason for increasing the word length of a digital system beyond 1 bit is to achieve a reduction in quantization noise. A 1-bit digital system has a signal to noise ratio (SNR) of less than 6 dB. In a 1-bit DSD system, the quantization noise is "shaped" or moved into ultrasonic frequencies so that the audible band can achieve an SNR that approaches 120 dB. To make this work, the sample rate of the 1-bit system must be very high so that there is adequate ultrasonic spectral space to place the quantization noise. This high sample rate 1-bit solution is a very inefficient and cumbersome approach to the problem. Nevertheless, DSD proves that long word lengths are not necessary to achieve high resolution!
Add a bit, add 6 dB
Every bit that is added to the word length increases the system SNR by about 6 dB (when measured over the entire Nyquist bandwidth of the digital system). The Nyquist bandwidth is equal to 1/2 of the sample rate and it defines the absolute limits of the frequencies that can be conveyed by a digital system. We can improve the audio-band SNR by increasing the word length, by increasing the sample rate, or by increasing both. In all cases, a properly-dithered digital system has infinite amplitude resolution (just like any analog system). When properly dithered, the errors produced by digital quantization produce nothing other than white noise! This surprising fact is unknown to many, and has led to the "resolution myth".
How good is the CD system?
A 16-bit system can achieve a 16 x 6 dB = 96 dB SNR over its entire bandwidth. TPDF dither (a common form of random white-noise dither) reduces this by about 3 dB, rendering a system with a usable SNR of about 93 dB. If the sample rate is 44.1 kHz (as used on all CDs) the Nyquist bandwidth is 22.05 kHz. This means that the combined dither and quantization noise will be spread evenly over this 22.05 kHz bandwidth, which is very close to the 20 KHz "audible" bandwidth. In a CD digital system, very little noise is hidden above the audible band, and the amplitude response is continuous (if properly dithered). The limitations of the CD are the 93 dB SNR and the 22.05 kHz bandwidth. One could argue that these numbers may limit the performance of the audio chain, and may produce some audible noise and audible limitation on the upper frequencies that may be partially detectable by some listeners. The CD was designed to just barely match the limitations of the human ear. Many would argue that it falls just slightly short of that goal. When it was introduced, the CD was hailed as "perfect audio forever".
How good is the DSD system?
DSD hides tremendous amounts of noise between 20 kHz and its Nyquist limit of 1.4112 MHz. For this reason, the ultrasonic noise in a DSD system can cause significant problems for power amplifiers and speaker transducers if it is not removed. To prevent these problems, 50 kHz low-pass filters are required at the output of DSD D/A converters. DSD achieves a 120 dB SNR with a usable bandwidth of 50 kHz. This is equivalent to a 20 to 21-bit system operating at a sample rate of 90 to 100 kHz. DSD can deliver higher performance than the 16-bit CD system.
What happens if we extend the word length to 24 bits?
24-bit digital systems can achieve an SNR of 144 dB (24 x 6 dB) over their Nyquist bandwidth. Again, TPDF dither will reduce this by about 3 dB. Even so, the 141 dB noise performance of a 24-bit digital transmission system is nothing less than spectacular. This noise performance exceeds the SNR of microphones, amplifiers, and our ears by at least 10 dB. This means that a 24-bit digital transmission system is more than adequate to transmit the very highest-quality recordings that we can produce or hear. The 24-bit digital channel also exceeds the noise performance of the 24-bit A/D and D/A converters at each end of the chain by at least 10 dB. Bottom line, 24-bit transmission systems will never add audible noise to a recording if the recorded peaks are reasonably near the clip point of the digital system. If there is an audible noise limitation it will be caused by the converters or the rest of the audio chain. The 24-bit PCM system does not constitute a noise limitation in any practical system. Digital audio systems exceeding 24-bits are only useful for processing in the studio where many cascaded 24-bit DSP operations could begin to create audible noise.
What happens if we increase the sample rate of our 24-bit system?
If we double the sample rate of our 24-bit system to a sample rate that is twice the rate used on CDs we reach a sample rate of 88.2 kHz. This gives us a Nyquist bandwidth of 44.1 kHz. This means that we can record and play musical content at frequencies up to 44.1 kHz (well beyond what is normally considered "audible"). But, this higher sample rate also means that the digital quantization noise is spread evenly over twice the bandwidth. This spreading of the noise means that there is less noise in the audible 20 kHz bandwidth. Doubling the sample rate improves the noise performance by 3 dB. Quadrupling the sample rate improves the noise performance by 6 dB. From a noise standpoint, quadrupling the sample rate is equivalent to adding 1 bit. Please note that a quadrupling of the sample rate also quadruples the file size of a digital recording. Adding 1 bit to a 24-bit system would only increase the file size by 4%. For this reason, sample rates should not be increased in an effort to improve noise performance. Sample rates should only be increased enough to accurately transmit all of the frequencies that are detectable by our auditory systems.
Summary - Its all About Noise
24-bit word lengths provide a very efficient method of improving the noise performance of digital systems. When dither is properly applied, there is no advantage to long word lengths other than improving the noise performance. Quantization errors in a properly-dithered digital system produce nothing other than random noise. Properly-dithered digital systems have infinite amplitude resolution.
Long word lengths do not improve the amplitude "resolution" of digital systems, they only improve the noise performance. But, noise can mask low-level musical details, so please do not underestimate the importance of a low-noise audio system.
John Siau
Leave a comment
Comments will be approved before showing up.
Also in Audio Application Notes

How Loud is the Distortion from Your Power Amplifier?
by John Siau August 08, 2025
Would you put a Washing Machine in your Listening Room?
If the answer is no, you may be surprised to discover that the distortion produced by your power amplifier may be louder than the noise produced by a major appliance.
Don't believe me? Take a look at Stereophile's test reports:
We selected 7 power amplifiers from Stereophile's top list of recommended amplifiers.
We took Stereophile's "THD+N vs. Power" plots for each, and replotted the data in a format that shows the loudness of the THD+N at the listening position.
The results are shocking!
Amplifier THD+N is louder than expected!
The distortion from your amplifier may be louder than a washing machine on the spin cycle, or it may be totally silent. How does yours perform? The answer is hidden in Stereophile's THD+N plots.
This application note reveals the hidden truth:
"The Distortion from your Power Amplifier may be Louder than a Washing Machine!"
I know, it sounds crazy, but this is what the measurements show!
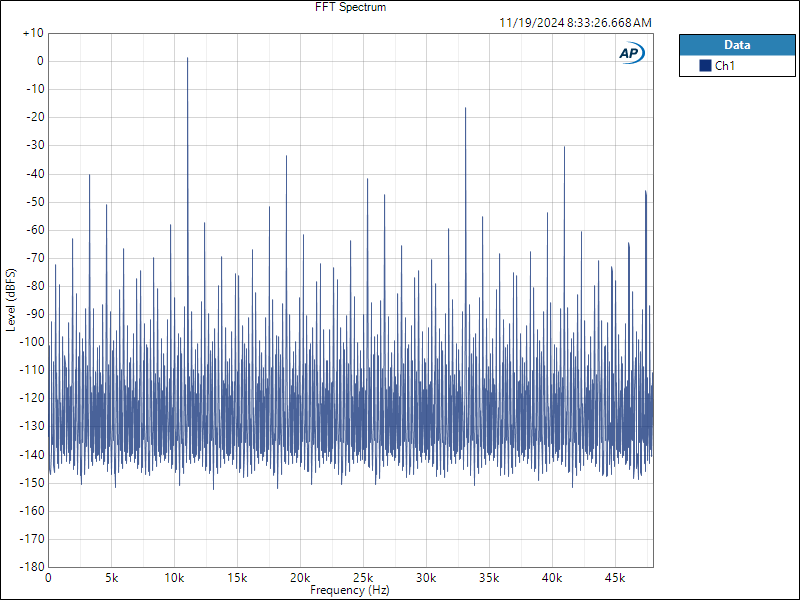
Interpolator Overload Distortion
by John Siau November 20, 2024
Most digital playback devices include digital interpolators. These interpolators increase the sample rate of the incoming audio to improve the performance of the playback system. Interpolators are essential in oversampled sigma-delta D/A converters, and in sample rate converters. In general, interpolators have vastly improved the performance of audio D/A converters by eliminating the need for analog brick wall filters. Nevertheless, digital interpolators have brick wall digital filters that can produce unique distortion signatures when they are overloaded.
10% Distortion
An interpolator that performs wonderfully when tested with standard test tones, may overload severely when playing the inter-sample musical peaks that are captured on a typical CD. In our tests, we observed THD+N levels exceeding 10% while interpolator overloads were occurring. The highest levels were produced by devices that included ASRC sample rate converters.

Audiophile Snake Oil
by John Siau April 05, 2024
The Audiophile Wild West
Audiophiles live in the wild west. $495 will buy an "audiophile fuse" to replace the $1 generic fuse that came in your audio amplifier. $10,000 will buy a set of "audiophile speaker cables" to replace the $20 wires you purchased at the local hardware store. We are told that these $10,000 cables can be improved if we add a set of $300 "cable elevators" to dampen vibrations. You didn't even know that you needed elevators! And let's not forget to budget at least $200 for each of the "isolation platforms" we will need under our electronic components. Furthermore, it seems that any so-called "audiophile power cord" that costs less than $100, does not belong in a high-end system. And, if cost is no object, there are premium versions of each that can be purchased by the most discerning customers. A top-of-the line power cord could run $5000. One magazine claims that "the majority of listeners were able to hear the difference between a $5 power cable and a $5,000 power cord". Can you hear the difference? If not, are you really an audiophile?

