Buy one component and save 10% on up to 2 cables. Buy 2 components and get 4 free cables. Free shipping on USA orders over $700. We are closed 1/1/26 and 1/2/26.
Buy one component and save 10% on up to 2 cables. Buy 2 components and get 4 free cables. Free shipping on USA orders over $700. We are closed 1/1/26 and 1/2/26.
Why "Audio Goes to 11"
by John Siau April 17, 2014

By John Siau
April 17, 2014
In my last post, "Audio that Goes to 11", I made the bold assertion that most of our audio recordings contain peaks that exceed the limits of our digital hardware. In this post I will show how this happens, and explain why this is a problem in PCM audio systems. In a must-see short video clip from "This is Spinal Tap", heavy-metal guitar player Nigel Tufnel eloquently explains that his Marshal amps "go to 11 ... one higher than 10".
The 16-bit digital system used on CD recordings can quantize audio into one of 65,536 levels (-32,768 to +32,767). But, to keep things simple, we will adopt Nigel's "0" to "10" scale. In a 16-bit system "10" is really 32,767, and "-10" is really -32,768. Here is how it looks:
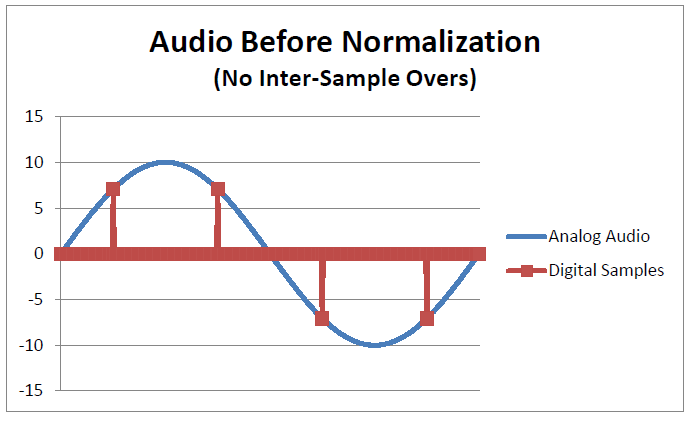
We have sampled an analog audio signal (blue trace). The digital samples are shown in red. Samples are an instantaneous snapshot of a continuous waveform. Our "snapshots" show two samples at about +7 followed by two samples at -7. Note that the input audio is just reaching "10", but the samples only reach "7". Our digital sampling system has missed the peaks and is erroneously showing a peak value of 7 instead of 10.
The amazing thing is that the analog peaks at +10 and -10 are not really lost. We can reconstruct an exact replica of the original analog sine wave, at exactly the correct amplitude using the interpolation and reconstruction filters that are normally incorporated into a DAC. Interpolation recovers the missing information between samples. Interpolation looks like this:

Life would be good if we never exceeded "7" on Nigel's scale. Nothing would ever clip because we would be allowing ample headroom in our digital system. In practice, this NEVER happens.
Nearly all commercial recordings use a process know as "normalization" to boost the audio to maximize the use of the dynamic range of our digital systems. Typically, each digital track is scanned to find the highest sample code in the track. Once this highest code is found, the entire track is turned up until the highest sample just reaches the maximum code. CD's are normalized so that peak codes just reach +32,767 or -32,768. The following chart shows this using a simplified -10 to +10 scale:
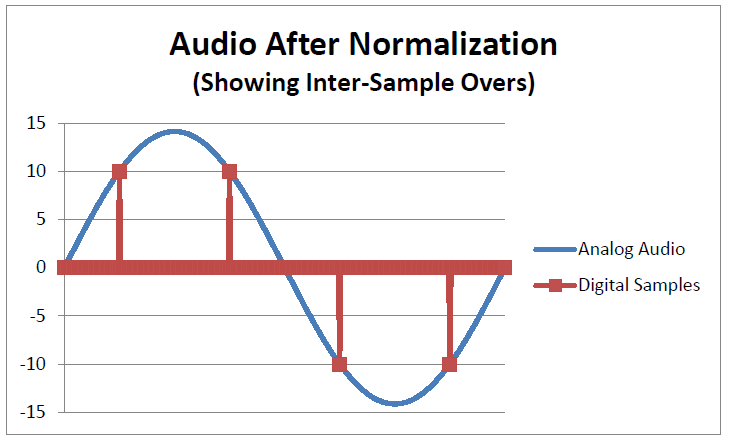
We now have digital samples reaching "10" and "-10". Our samples don't exceed "10", so we have not clipped our digital storage system. We have maximized the loudness of our recording and are now maximizing the use of our digital storage system. Life is good - almost.
The problem occurs when we try to play this normalized audio. The DAC will apply interpolation to reconstruct the original waveform. This time, we encounter a problem. The interpolator clips at "10". Here is the result:
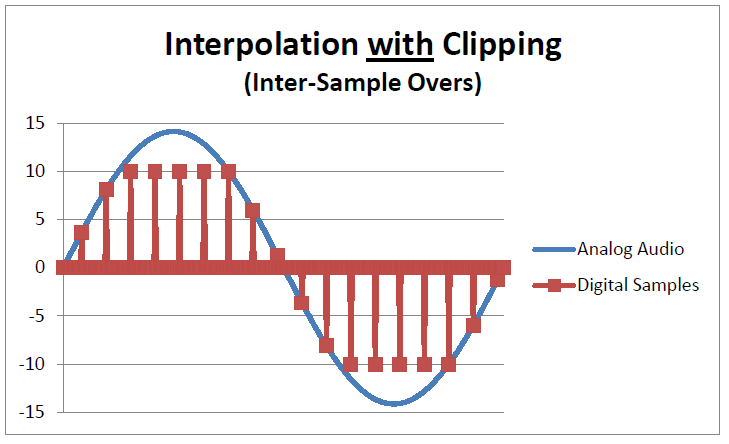
The interpolation filter has clipped the waveform and is now generating high levels of distortion. Our digital system has failed to deliver the "perfect sound" that was claimed when the CD was introduced. Does this mean that PCM audio is broken? Should we move to DSD to eliminate interpolation filters? What is the answer?
The answer is headroom. All signal processing steps in the audio chain need headroom. We need headroom in the analog sections, and we need headroom in the digital signal processing.
If we add the required headroom to the interpolation filter we get the following results:

With adequate headroom, the DAC accurately reproduces audio "going to 14". The inter-sample overs are not clipped and distortion is avoided.
Our DACs go to 14
If we are going to use Nigel's scale, I guess you could say "our DACs go to 14"! The Benchmark DAC2 and DAC3 series converters have 3.5 dB of headroom above 0 dBFS.
It is my opinion that the clipping of inter-sample overs is a major issue. The solution is not to eliminate interpolation filters. The solution is headroom. Benchmark added this additional headroom starting with the DAC2 series converters.
Additional Reading:
"Overload in Signal Conversion", Nielsen and Lund, TC Electronics (PDF)
"Over The Top - Measured Results", Jim Lesurf, AudioMisc
"Avoiding Inter Sample Peaks", des, Hometracked.com
Also in Audio Application Notes

How Loud is the Distortion from Your Power Amplifier?
by John Siau August 08, 2025
Would you put a Washing Machine in your Listening Room?
If the answer is no, you may be surprised to discover that the distortion produced by your power amplifier may be louder than the noise produced by a major appliance.
Don't believe me? Take a look at Stereophile's test reports:
We selected 7 power amplifiers from Stereophile's top list of recommended amplifiers.
We took Stereophile's "THD+N vs. Power" plots for each, and replotted the data in a format that shows the loudness of the THD+N at the listening position.
The results are shocking!
Amplifier THD+N is louder than expected!
The distortion from your amplifier may be louder than a washing machine on the spin cycle, or it may be totally silent. How does yours perform? The answer is hidden in Stereophile's THD+N plots.
This application note reveals the hidden truth:
"The Distortion from your Power Amplifier may be Louder than a Washing Machine!"
I know, it sounds crazy, but this is what the measurements show!
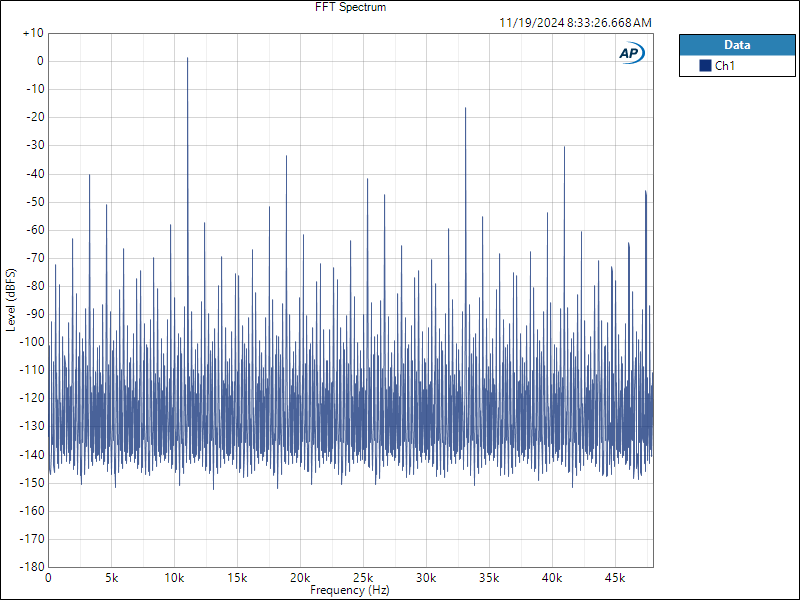
Interpolator Overload Distortion
by John Siau November 20, 2024
Most digital playback devices include digital interpolators. These interpolators increase the sample rate of the incoming audio to improve the performance of the playback system. Interpolators are essential in oversampled sigma-delta D/A converters, and in sample rate converters. In general, interpolators have vastly improved the performance of audio D/A converters by eliminating the need for analog brick wall filters. Nevertheless, digital interpolators have brick wall digital filters that can produce unique distortion signatures when they are overloaded.
10% Distortion
An interpolator that performs wonderfully when tested with standard test tones, may overload severely when playing the inter-sample musical peaks that are captured on a typical CD. In our tests, we observed THD+N levels exceeding 10% while interpolator overloads were occurring. The highest levels were produced by devices that included ASRC sample rate converters.

Audiophile Snake Oil
by John Siau April 05, 2024
The Audiophile Wild West
Audiophiles live in the wild west. $495 will buy an "audiophile fuse" to replace the $1 generic fuse that came in your audio amplifier. $10,000 will buy a set of "audiophile speaker cables" to replace the $20 wires you purchased at the local hardware store. We are told that these $10,000 cables can be improved if we add a set of $300 "cable elevators" to dampen vibrations. You didn't even know that you needed elevators! And let's not forget to budget at least $200 for each of the "isolation platforms" we will need under our electronic components. Furthermore, it seems that any so-called "audiophile power cord" that costs less than $100, does not belong in a high-end system. And, if cost is no object, there are premium versions of each that can be purchased by the most discerning customers. A top-of-the line power cord could run $5000. One magazine claims that "the majority of listeners were able to hear the difference between a $5 power cable and a $5,000 power cord". Can you hear the difference? If not, are you really an audiophile?

