System Performance Calculations
If an audio system is composed of multiple components, we may have detailed specifications for each component, but we will not know the performance of the combined system without doing some calculations.
Questions
We may want to answer system-level questions such as these:- How loud will my audio system play?
- Will my audio system produce audible noise?
- Will my audio system produce audible distortion?
- How will my audio components work together as a system?
If we have specifications for each component, we can begin to answer these questions.
How loud will my audio system play?
If we know the output power of an amplifier, as well as the sensitivity and impedance of our loudspeakers, we can calculate the maximum sound pressure level that our system can produce. This calculation will require conversions between linear and logarithmic units. It may also require conversions between voltage and power units. The math is not difficult, but it can be confusing. The bottom line is that most users will never make these calculations before selecting audio components.
I have created a series of calculators that can be used to calculate the system performance of any amplifier/speaker combination if a few basic specifications are known. Here is one example:
Peak SPL Calculator
This example shows that a 100W amplifier can deliver a 110 dB peak SPL (sound pressure level) at the listening position when driving speakers with a 90 dB voltage sensitivity. These values are typical for many hi-fi systems. This simplified calculator assumes a stereo configuration, a 2-meter listening distance, and a typical listening room.
Is a peak level of 110 dB SPL adequate for a hi-fi system?
In most cases, the answer is yes.
Dolby-approved professional mix rooms must be capable of delivering 105 dB SPL peaks in order to achieve an 85 dB SPL calibrated listening level. These professional environments are designed to have 20 dB of headroom above the desired average listening level. In a home environment, a 100 dB peak output may be sufficient. This will provide headroom for 15 dB peaks above the 85 dB (average SPL) corresponding to the Dolby listening level for movies.
In general, a home hi-fi system should be designed to achieve a peak SPL of at least 100 dB. A minimum peak output of 105 to 110 dB SPL is probably a better target range, especially if the music system will also be used while watching movies. The 110 dB peak output of the example system will provide a very generous amount of headroom, even when listening to movies.
Enter the values for your own speakers and power amplifier, and then click "calculate" to estimate the peak SPL at a typical listening position. If your system output is less than 100 dB SPL, it is probably underpowered. If you find that you occasionally reach clipping, you should move to a higher powered amplifier or to a more efficient set of speakers.
Converting Power Sensitivity to Voltage Sensitivity
Check the units that are used to quantify the sensitivity of your speakers. The units are often db SPL at a power of 1 watt and a distance of 1 meter (dB @1W/1m). But loudspeakers are voltage driven devices and it is much better to specify the voltage sensitivity because this takes the speaker impedance out of the equation. Voltage sensitivity is specified as dB SPL at 2.83 V and a distance of 1 meter (dB@2.83V/1m). These units are interchangeable when the speaker has an 8-ohm impedance. The reason for this is that it takes a drive voltage of 2.83 volts to deliver 1 watt of power into an 8-ohm load.
If your speakers have an impedance other than 8 Ohms, and the sensitivity is specified in terms of power, you will need to use the "Speaker Sensitivity Calculator" below to convert power sensitivity to voltage sensitivity:
Speaker Sensitivity Converter
If necessary, run this conversion for your speakers, and then recalculate the peak SPL for your system. Notice that you must enter your speaker impedance when using this calculator.
Adjusting for the listening room
A more advanced peak SPL calculator adds selections for the number of speakers, the listening distance, and the room configuration. Enter your system parameters and your listening distance to make a more accurate estimate of your system's peak SPL capabilities. This calculator shows each of the factors that contribute to the SPL at the listening position. Give it a try with the default values and then enter the parameters for your own system and listening space:
Peak SPL Calculator - Advanced
Will my audio system produce audible noise?
We can look at an amplifier/speaker combination and calculate the sound pressure level of the noise that will be emitted from our speakers due to the noise produced by the power amplifier. If the result is less than 0 dB SPL, the noise should be inaudible since it falls below the threshold of normal hearing. If the noise rises above 0 dB SPL it will be audible if the room is reasonably quiet.
Example 1 - typical 100 W amplifier driving 95 dB speakers
The highlighted numbers are already entered in the calculator. Press "calculate" to see the results.
- Brand X stereo amplifier - SNR = 105 dB
- 8-Ohm output power = 100 W
- Speakers with a 95 dB sensitivity at 2.83 V
- Result = 10 dB SPL Noise Level
Give this calculator a try with the default values (which are typical for many hi-fi systems). You will find that the noise SPL at the listening position is 10 dB above the threshold of normal hearing. The amplifier noise may be audible with this amplifier-speaker combination if the room is reasonably quiet. The audibility of the noise will increase as you move closer to the speakers.
Noise Audibility Calculator
Try these additional examples using the "Noise Audibility Calculator":
Example 2 - typical 400 W amplifier driving 95 dB speakers
The highlighted numbers are already entered in the calculator. Change the power to 400 W and then press "calculate" to see the results of increasing the amplifier power by a factor of 4.
Enter the highlighted numbers and press "calculate" to see the results:
- Brand X stereo amplifier - SNR = 105 dB
- 8-Ohm output power = 400 W
- Speakers with a 95 dB sensitivity at 2.83 V
- Result = 16 dB SPL Noise Level
In this example, the added amplifier power raises the output noise by 6 dB. The noise is now 16 dB above the threshold of hearing. This example shows that larger power amplifiers need to have a better SNR to achieve similar noise performance. A 4x increase in power will require a 6 dB improvement in SNR to achieve the same noise levels at the output of the speakers.
Example 3 - Benchmark AHB2 (stereo) - 100 W driving 95 dB speakers
In stereo mode, the Benchmark AHB2 has a SNR of 132 dB at an output power of 100 W.
Enter the highlighted numbers and press "calculate" to see the results:
- Benchmark AHB2 stereo amplifier - SNR = 132 dB
- 8-Ohm output power = 100 W
- Speakers with a 95 dB sensitivity at 2.83 V
- Result = -17 dB SPL Noise Level
Example 3 shows that the noise produced by the amplifier, and delivered by the speakers, will be 17 dB below the threshold of hearing at the listening position. Given this performance, you will find that there is no audible noise at a point-blank range from the speakers. You can walk up to the speakers without hearing any noise.
Example 4 - Benchmark AHB2 (mono) - 380 W driving 95 dB speakers
The Benchmark AHB2 delivers almost 4 times as much power in the bridged mono mode. In bridged mono mode, the AHB2 has a SNR of 135 dB at 380 W.
Enter the highlighted numbers and press "calculate" to see the results:
- Benchmark AHB2 mono amplifier - SNR = 135 dB
- 8-Ohm output power = 380 W
- Speakers with a 95 dB sensitivity at 2.83 V
- Result = -14 dB SPL Noise Level
The -14 dB SPL result shows that the AHB2 is still dead quiet, when configured to deliver 380 Watts at a peak SPL of 121 dB.
Example 5 - Benchmark AHB2 (mono) - 380 W driving 105 dB speakers
If we replace the 95 dB speakers with a set of high-efficiency horn-loaded speakers, you can see why we designed the AHB2 to be so quiet.
Enter the highlighted numbers and press "calculate" to see the results:
- Benchmark AHB2 mono amplifier - SNR = 135 dB
- 8-Ohm output power = 380 W
- Speakers with a 105 dB sensitivity at 2.83 V
- Result = -4 dB SPL Noise Level
The -4 dB SPL result shows that the AHB2 is still dead quiet, when configured to deliver 380 Watts at a peak SPL of 131 dB. Such a system matches the limits of human hearing. It would produce no audible noise when idle and yet it could reach the threshold of pain at full output.
These calculations show that amplifiers with a 105 dB SNR can be expected to produce some audible noise while the Benchmark AHB2 can be expected to be absolutely silent with any speaker configuration.
Will my audio system produce audible distortion?
This is a difficult question to answer!
We can look at an amplifier/speaker combination and calculate the sound pressure level of the THD+N (total harmonic distortion plus noise) that will be emitted from our speakers due to the THD+N produced by the power amplifier. If the result is less than 0 dB SPL, it should be completely inaudible since it falls below the threshold of normal hearing. If it rises above 0 dB SPL, the situation begins to get very complicated. At some threshold above 0 dB SPL, the electronically produced distortion will start to become audible. Under the right circumstances, the music may mask the THD+N until it reaches levels well above 0 dB SPL, but this is not always the case. Unfortunately, it is very hard to predict the threshold at which THD+N will become audible while music is playing. This threshold of audibility is continually changing as the music plays.
How good is good enough?
How low does THD+N need to be in order to be inaudible? We can't answer this question because we don't know all of the variables. We don't know what music or type of music will be played, nor does a single THD+N number give us any indication of how the distortion products are distributed across audible frequencies. The music will mask some or even all of the THD+N, but we don't know the threshold where this masking will begin to fail. Again, this threshold is continually changing while the music is playing.
The best we can say about the threshold of masking is this:
- THD+N above the 0 dB SPL threshold of hearing may be audible if it is not masked.
- Music may mask THD+N at levels that are much higher than 0 dB SPL.
- THD+N masking thresholds are continually changing.
Do we really want an audio system that only sounds good when its defects are masked by the music? Can we build an audio system that will never produce electronically generated THD+N exceeding the threshold of hearing? If this is possible, then we can have confidence in the transparency of our electronics. Instead of focusing on uncertainties of masking, lets determine if it is possible to reduce defects to a level that is below the threshold of hearing.
We can say the following with confidence:
- THD+N is completely inaudible if it is below the 0 dB SPL threshold of hearing.
If we can keep the electronically generated THD+N below 0 dB SPL, we do not need to concern ourselves with the uncertainties of masking. Some would argue that this is overkill and that it will add unnecessary expense to the audio system. Others would suggest that this performance is not even possible. The correct answer is that this goal is within the capabilities of today's technology.
Benchmark takes a conservative approach to THD+N. Our goal is to design our systems such that the THD+N due to the electronics is less than 0 dB SPL at the listening position. We have the technology to keep THD+N near or below the 0 dB SPL threshold of hearing, and we can do this at a reasonable price point, so why not do it? We will plug some numbers into the "THD+N Audibility Calculator" (below) to explore this claim.
If you run the calculations, you will find that the THD+N produced by an entire Benchmark signal chain is below or just slightly above 0 dB SPL at the listening position. There will be audible THD from the loudspeakers (at much higher levels), and there may be audible THD from the recording and studio equipment, but there will be no audible THD+N produced by the Benchmark playback electronics. This is what we mean when we say that Benchmark products are designed to be transparent.
Try the same calculations with the THD+N specifications from many other products and you will find that many will deliver electronically produced distortion at levels well above the 0 dB SPL threshold of hearing.
Again, if the THD+N is near 0 dB SPL it is very likely that it will be entirely masked by the music. But, if the THD+N is 50 or 60 dB above 0 dB SPL it is very unlikely that it will be completely masked by the music.
THD+N audibility is also a function of which harmonics are produced by the system. Higher order harmonics are often easier to hear than low order harmonics since the fundamental tone is many octaves below the high order harmonics. For example, if a 100 Hz tone is played and the amplifier creates a strong 5th harmonic, this will fall at 500 Hz and it will be outside of the masking provided by the 100 Hz tone.
Given the above discussion, lets take a conservative approach, and restate the THD+N audibility question as follows:
Will my system electronics produce THD+N exceeding 0 dB SPL?
We can answer this question using Benchmark's "THD+N Audibility Calculator" (below). Enter the numbers given in the examples below, or enter numbers corresponding to your system.
Example 6 - AHB2 in Stereo Mode
The highlighted numbers are already entered in the calculator. Press "calculate" to see the results.
- Benchmark AHB2 Amplifier, stereo mode - THD+N < -110 dB
- 8-Ohm output power = 100 W
- Speakers with a 90 dB sensitivity at 2.83 V
- Result = 0 dB SPL
This result shows that the THD+N produced by the AHB2 will just reach the threshold of hearing at the full 100 W output power. At 0 dB SPL, the THD+N is absolutely inaudible. You could not even hear the distortion if it could be played while the music was muted.
THD+N Audibility Calculator
Try these additional examples using the "THD+N Audibility Calculator":
Example 7 - AHB2 in Mono Mode
Enter the highlighted numbers and press "calculate" to see the results:
- Benchmark AHB2 Amplifier, mono mode - THD+N < -110 dB
- 8-Ohm output power = 380 W
- Speakers with a 90 dB sensitivity at 2.83 V
- Result = 6 dB SPL (Just above the threshold of hearing, completely inaudible when the music is playing)
Example 8 - 100W at 1% THD+N
Enter the highlighted numbers and press "calculate" to see the results:
- Brand X Amplifier - THD+N < 1% at 100 W
- Convert 1% to dB using the "THD % to dB Converter" (bottom of page)
- 1% converts to -40 dB (enter this value)
- 8-Ohm output power = 100 W
- Speakers with a 90 dB sensitivity at 2.83 V
- Result = 70 dB SPL (The distortion is loud!)
Example 9 - 100W at 0.01% THD+N
Enter the highlighted numbers and press "calculate" to see the results:
- Brand Y Amplifier - THD+N < 0.01% at 100 W
- Convert 0.01% to dB using the "THD % to dB Converter" (bottom of page)
- 0.01% converts to -80 dB (enter this value)
- 8-Ohm output power = 100 W
- Speakers with a 90 dB sensitivity at 2.83 V
- Result = 30 dB SPL (The distortion is well above the threshold of hearing and may not be fully masked by the music).
THD % to dB Converter
Use this converter to convert % THD+N to dB THD+N:
Think dB and not percent!
Distortion measurements (THD, THD+N and IMD) are traditionally expressed in terms of percent. But what do 1%, 0.1%, 0.01% or 0.001% mean in terms of loudness or audibility?
If you are like most people you just know that 0.001% is the best of the three numbers listed above. If you are a well-trained geek you will recognize that each added leading zero represents a 20 dB improvement. 0.01% is 20 dB lower than 0.1% and this is 20 dB lower than 1%. The well-trained geek will convert % to dB in order to give meaning to these numbers. With the calculator above, you don't have to be a geek.
Use the "THD % to dB Converter" to convert 1%, 0.1%, 0.01% and 0.001% to dB (relative to the music).
When distortion reaches 1%, it is just 40 dB lower than the music (-40 dB). When distortion reaches 0.1%, it is 60 dB lower than the music (-60 dB). When distortion reaches 0.01%, it is 80 dB lower than the music (-80 dB). And, when the distortion reaches 0.001% it is 100 dB lower than the music (-100 dB). The -40 dB, -60 dB, -80 dB, and -100 dB figures should be easier to understand than 1%, 0.1%, 0.01% and 0.001%.
Read more here:
Also in Audio Application Notes
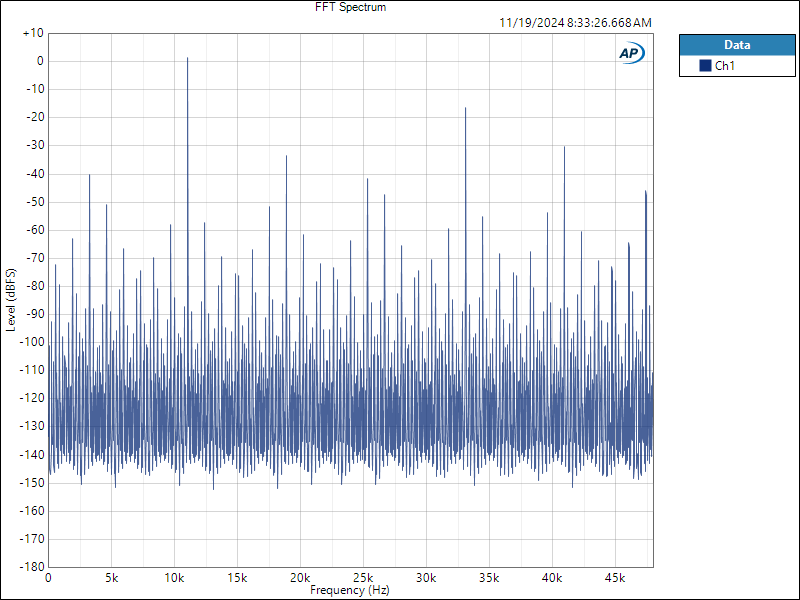
Interpolator Overload Distortion
Most digital playback devices include digital interpolators. These interpolators increase the sample rate of the incoming audio to improve the performance of the playback system. Interpolators are essential in oversampled sigma-delta D/A converters, and in sample rate converters. In general, interpolators have vastly improved the performance of audio D/A converters by eliminating the need for analog brick wall filters. Nevertheless, digital interpolators have brick wall digital filters that can produce unique distortion signatures when they are overloaded.
10% Distortion
An interpolator that performs wonderfully when tested with standard test tones, may overload severely when playing the inter-sample musical peaks that are captured on a typical CD. In our tests, we observed THD+N levels exceeding 10% while interpolator overloads were occurring. The highest levels were produced by devices that included ASRC sample rate converters.
Audiophile Snake Oil
The Audiophile Wild West
Audiophiles live in the wild west. $495 will buy an "audiophile fuse" to replace the $1 generic fuse that came in your audio amplifier. $10,000 will buy a set of "audiophile speaker cables" to replace the $20 wires you purchased at the local hardware store. We are told that these $10,000 cables can be improved if we add a set of $300 "cable elevators" to dampen vibrations. You didn't even know that you needed elevators! And let's not forget to budget at least $200 for each of the "isolation platforms" we will need under our electronic components. Furthermore, it seems that any so-called "audiophile power cord" that costs less than $100, does not belong in a high-end system. And, if cost is no object, there are premium versions of each that can be purchased by the most discerning customers. A top-of-the line power cord could run $5000. One magazine claims that "the majority of listeners were able to hear the difference between a $5 power cable and a $5,000 power cord". Can you hear the difference? If not, are you really an audiophile?
Making Sound with Plasma - Hill Plasmatronics Tweeter
At the 2023 AXPONA show in Chicago, I had the opportunity to see and hear the Hill Plasmatronics tweeter. I also had the great pleasure of meeting Dr. Alan Hill, the physicist who invented this unique device.
The plasma driver has no moving parts and no diaphragm. Sound is emitted directly from the thermal expansion and contraction of an electrically sustained plasma. The plasma is generated within a stream of helium gas. In the demonstration, there was a large helium tank on the floor with a sufficient supply for several hours of listening.
While a tank of helium, tubing, high voltage power supplies, and the smell of smoke may not be appropriate for every living room, this was absolutely the best thing I experienced at the show!
- John Siau